Ieškoti Furlier serijos koeficientų. Nuskaitymo koeficientų nustatymas Fourier Formules

Furjė serija periodinių funkcijų su 2π laikotarpiu.

"Fourier" serija leidžia studijuoti periodines funkcijas, suskaidydami juos į komponentus. Kintamieji ir įtampa, poslinkiai, greitis ir pagreitis alkūninių jungiamųjų mechanizmų ir akustinių bangų yra tipiški praktiniai pavyzdžiai periodinių funkcijų naudojimo inžinerinių skaičiavimų naudojimo.

Furjė skilimas grindžiamas prielaida, kad visa praktinė funkcijos vertė intervalo ≤ ≤X≤ π gali būti išreikšta susiliečiančių trigonometrinių eilučių pavidalu (skaičius yra susilieja, jei susideda iš dalinių sumų seka savo narių konverges:

Standartinis (\u003d normalus) įrašymas per SINX ir COSX sumą

f (x) \u003d a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...

kur O, A 1, A2, ..., B 1, B 2, .. - Galiojančios konstantos, t.e.

Kur yra nuo -π iki π koeficientų eilutė Apskaičiuojamas pagal formules:

COEFICATIONS A O, A N ir B N yra vadinami furjė koeficientaiir jei jie gali būti rasti, tada yra vadinamas numeris (1) netoli Fourier, Atitinkamos funkcijos f (x). Už numerį (1), narys (a 1 cosx + b 1 sinx) yra vadinamas pirmiausia arba pagrindinė harmonika

Kitas būdas įrašyti numerį yra naudoti ACOSX + BSINX \u003d CSIN santykį (X + α)

f (x) \u003d A O + C1 sin (x + α 1) + C2 sin (2x + α 2) + ... + C n sin (NX + α n)

Kur Ao yra pastovus, C1 \u003d (A 1 2 + B 1 2) 1/2, su n \u003d (2 + Bn 2) 1/2 - įvairių komponentų amplitudė ir yra AN \u003d ARCTG AN / B n.

Už numerį (1), narys (a 1 cosx + b 1 sinx) arba C1 sin (x + α 1) yra vadinamas pirmuoju arba pagrindinė harmonika (A 2 COS2X + B 2 SIN2X) arba C 2 SIN (2x + α 2) vadinamas antroji harmonika ir tt

Tiksliam kompleksinio signalo pristatymui paprastai reikalingas begalinis narių skaičius. Tačiau daugeliu praktinių užduočių pakanka tik apsvarstyti tik keletą pirmųjų narių.

Furjė serija nepereinamų funkcijų su 2π laikotarpiu.

Periodinių funkcijų apibrėžimas.

Jei funkcija f (x) yra ne periodinė, tai reiškia, kad jis negali būti suskaidytas į fourier serijos visas vertes x. Tačiau galite apibrėžti "Fourier" seriją, atstovaujančią bet kokio 2π pločio diapazone.

Jei nenurodyta ne periodinė funkcija, galite sukurti naują funkciją, pasirinkdami F (x) reikšmes į konkrečią diapazoną ir pakartokite juos iš šio intervalo su 2π intervalu. Kadangi nauja funkcija yra periodinė su 2π laikotarpiu, jis gali būti suskaidytas į "Fourier" seriją visoms x. Pavyzdžiui, funkcija f (x) \u003d x nėra periodinė. Tačiau, jei būtina jį suskirstyti į Fourier serijos intervalu nuo maždaug 2π, tada periodinė funkcija su 2π laikotarpiu yra pastatytas už šio intervalo (kaip parodyta Fig. Žemiau).

Neperminuotoms funkcijoms, pvz., F (x) \u003d x, Furjė serijos suma yra lygi f (x) visuose nurodyto diapazono taškuose, tačiau jis nėra lygus f (x) taškams už diapazono ribų. Jei norite rasti "Fourier" eilutę apie ne periodinę funkciją 2π diapazone, naudojama Furjė koeficientų formulė.

Net ir nelygios funkcijos.

Jie sako, kad funkcija y \u003d f (x) netJei f (-x) \u003d f (x) visoms reikšmėms x. Netgi funkcijų grafikai visada yra simetriški su ašia y (t) atspindi veidrodis). Du netgi funkcijų pavyzdžiai: y \u003d x 2 ir y \u003d cosx.

Sakoma, kad funkcija y \u003d f (x) nelyginisjei f (-x) \u003d - f (x) visoms reikšmėms x. Nelyginių funkcijų diagramos visada yra simetriškos, palyginti su koordinatės pradžia.

Daug funkcijų nėra nei net ir keista.

Skišė fourier serijos cosine.

Furjė serijos net periodinės funkcijos f (x) su 2π laikotarpiu yra tik nariai su cosine (t.e. neturi narių su sinusais) ir gali būti nuolatinis narys. Taigi,

kur "Furjier" serijos koeficientai

Furjė serijos nelyginio periodinės funkcijos F (x) su 2π laikotarpiu yra tik nariai su Sinus (t.e. neturi narių su Cosine).

Taigi,

kur "Furjier" serijos koeficientai

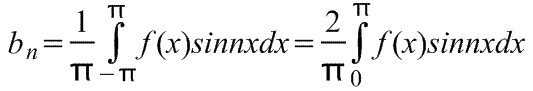
Fourier eilutė ant pusės Aode.

Jei funkcija yra apibrėžta diapazonui, pvz. Gauta "Furjier" serija vadinama artimiausioje pusėje.

Jei norite gauti skilimą Fourier ant pusiau kosinofunkcijos f (x) diapazone nuo 0 iki π, būtina atlikti net periodinę funkciją. Fig. Žemiau yra funkcija f (x) \u003d x, pastatyta ant intervalo nuo x \u003d 0 iki x \u003d π. Kadangi netgi funkcija yra simetriška, atsižvelgiant į ašį F (x), atlikite AB liniją, kaip parodyta Fig. žemiau. Jei manote, kad už laikomo intervalo ribų, gauta trikampė forma yra periodinė su 2π laikotarpiu, tada galutinis grafikas turi formą, šou. Fig. žemiau. Kadangi reikia gauti keturis kartus skilimą cosine, kaip ir anksčiau, apskaičiuoti keturračius koeficientus a o ir n

Jei reikia gauti fourier skilimas pusiau sinais Funkcijos f (x) diapazone nuo 0 iki π, tada būtina atlikti nelyginę periodinę funkciją. Fig. Žemiau yra funkcija f (x) \u003d x, pastatyta intervale nuo x \u003d 0 iki x \u003d π. Kadangi nelyginė funkcija yra simetriška, palyginti su koordinatės pradžia, sukuriame CD liniją, kaip parodyta Fig. Jei manome, kad už laikomo intervalo ribų, gauta pjautinė signalas yra periodinis su 2π laikotarpiu, tada galutinis grafikas turi Fig. Kadangi reikia gauti rūstybės skilimą pusiau sinarai, kaip ir anksčiau, apskaičiuoti Furjė koeficientą. B.

Furjė serija savavališko intervalui.

Periodinės funkcijos skaidymas su L. laikotarpiu

Periodinė funkcija f (x) kartojama didinant x l, i.e. f (x + l) \u003d f (x). Perėjimas nuo anksčiau aptartų funkcijų su 2π funkcijomis su laikotarpiu l yra gana paprasta, nes ji gali būti padaryta pakeičiant kintamąjį.

Norėdami rasti "Fourier" seriją f (x) į -l / 2≤X≤L / 2 diapazone, pristatome naują kintamąjį u tokiu būdu, kad funkcija f (x) įvyksta 2π palyginti su U. Jei u \u003d 2πx / l, tada x \u003d -l / 2 ne u \u003d -π ir x \u003d l / 2 ne u \u003d π. Taip pat leiskite f (x) \u003d f (lu / 2π) \u003d f (u). Furjė serija f (u) turi vaizdą

(Integracijos ribos gali būti pakeistos bet kuriuo intervalu L ilgis, pavyzdžiui, nuo 0 iki L)

"Fourier" serija pusę laikotarpio funkcijoms, nurodytoms intervalui l ≠ 2π.

Pakaitui u \u003d πh / l, intervalas nuo x \u003d 0 iki x \u003d l atitinka intervalą nuo u \u003d 0 į u \u003d π. Todėl funkcija gali būti suskaidyta tik "Cosine" arba tik sinuso, t.y. į fourier serijos pusiau Aode.

Cosine skilimas nuo 0 iki aš turi formą

Vienas iš funkcinių serijų tipų yra trigonometrinė serija

Užduotis yra pasirinkti serijos koeficientus, kad ji būtų konvertuojant į intervalo funkcijas [-π, π]; Kitaip tariant, būtina suskaidyti šią funkciją trigonometrinėje eilutėje. Pakankama šios problemos sprendimo sąlyga yra ta, kad funkcija yra intervale [-π, π] nepertraukiamai ir dalijasi diferencijuojama, ty taip, kad intervalas [-π, π] būtų suskirstytas į ribotą dalinio numerį intervalai, kurių kiekviena ši funkcija yra nuolatinė ir turi darinį (dalinių intervalų galuose, funkcija turi būti baigtini vienpusių ribų ir vienpusių išvestinių finansinių priemonių, apskaičiuojant funkcijos funkciją dalinio pabaigoje intervalas, jo vienpusė riba yra priimta). Skirtingumo sąlyga gali būti pakeista funkcijos kūrinių monotonija, ty reikalavimas užtikrinti, kad funkcija būtų monotona kiekviename iš dalinių intervalų. Pakankama būklė skilimo funkcijai intervalo [-π, π] trigonometrinėje serijoje taip pat yra reikalavimas taip, kad šioje intervale funkcija turi ribotą pokytį. Pagal Funkcijos f (x) apibrėžimą intervale yra ribotas pokytis, jei su bet kuriuo šio intervalo skaidiniu iki galutinio skaičiaus intervalų

vertė

ribotas nuo to paties numerio.

Tai yra su tokiomis funkcijomis, kurios turi susidoroti su praktinių užduočių sprendimais.

Atliekant bet kurį iš trijų nurodytų pakankamos sąlygos Funkcija f (x) yra atstovaujama intervale [-π, π] trigonometriniai šalia, kurioje koeficientai nustato formules

Su tokiais koeficientais, trigonometrinė eilutė yra vadinama netoli Fourier. Ši serija susilieja su f (x) kiekvienu jo tęstinumo tašku; Pertraukų taškuose ji susilieja su vidutiniais aritmetiniais kairiais ir dešiniajomis ribinėmis vertėmis, t. Y K, jei X yra tarpo taškas (1 pav.); Segmento ribose yra numeris.

1 pav.

Funkcija, išreikšta šalia Fourier, yra periodinė funkcija, todėl skaičius, sudarytas už funkciją, nurodytą segmente [-π, π] konverguojant iš šio segmento į periodinį šios funkcijos tęstinumą (2 pav.).

2 pav.

Jei Furjė funkcija f (x) pateikiama savavališku intervalu [α, α + 2π] ilgio 2π, tada iš eilės koeficientai A 0, AK, BK (Furjė koeficientai) gali būti nustatomi pagal nurodytus formules, kuriose Integracijos ribos pakeičiamos α ir α + 2π. Apskritai, nes formulėse už 0, A K, B K, yra funkcijos su 2π laikotarpiu, integracija gali būti atliekama bet kuriuo intervalu su 2π ilgio.

"Fourier" serija gali būti naudojama apytiksliam funkcijos vaizdui, būtent: F (x) funkcija pakeičiama maždaug vienoda pirmųjų "Furtier" serijos narių s dydžio:

Išraiška SN (X), kur 0, AK, BK yra Fourier koeficientai f (x), palyginti su kitomis tos pačios rūšies išraiškomis su ta pačia verte N, bet su kitais koeficientais, sukelia minimalų vidutinį kvadratinį nuokrypį SN (X ) nuo f (x), kuris yra apibrėžiamas kaip

Priklausomai nuo funkcijos simetrijos rūšies, kai kurie supaprastinimai yra įmanomi. Jei funkcija yra lygus, t.y. f (-x) \u003d f (x), tada

ir funkcija suskaido į kosino eilutę. Jei funkcijos yra keista, t.y. f (-m) \u003d - f (x), tada

ir funkcija suskaido į sinuso eilutę. Jei funkcija atitinka f (x + π) \u003d - f (x), t.y. kreivė, susijusi su puse segmento 2π, yra kitos pusės kreivės atspindžio atspindys, \\ t

Funkcija gali būti nurodyta ne tik 2π ilgio segmente, bet ir bet kurio ilgio segmente 2L. Jei jis atitinka pirmiau minėtas sąlygas šiame segmente, jis yra išdėstytas fourier serijos šie tipo:

ir skaičiaus koeficientus apskaičiuoja formulės

Tab. 1 DANA kai kurių funkcijų skilimas.

1 lentelė.

Trigonometrinė eilutė gali būti užfiksuota šioje formoje:

"Fourier" serijos funkcija F (x) konverguojasi anksčiau, lygesnė funkcija. Jei funkcija f (x) ir jo dariniai F "(x), f" (x), ..., FK -1 (x) yra tęstiniai ir f (k) (x) leidžia tik atotrūkio taškus Galų gale "Furjier" koeficientai bus N, BN funkcijos f (x) bus

Simbolis yra pažymėtas tokiu dydžiu

Skilimas į trigonometrinę eilutę vadinama harmonine analize ir trigonometrinės funkcijosĮtraukta į šią seriją - harmonikai. Iš harmonikų komponentų skaičiavimas vadinamas harmoniniu sinteze.

Apskaičiuojant struktūras, dažnai būtina suskaidyti "Fourier" serijoje Įvairios funkcijosApibrėžti diagramose ir visų pirma vaizduojant apkrovą. Tab. 2 ir 3 skilimai pateikiami tam tikroms kroviniams būdingoms funkcijoms, įskaitant eilutes, atitinkančias koncentruotas jėgas.

2 lentelė.

Funkcijų grafikas	Fourier eilutė	n.

Transkriptas.

1 Švietimo ir mokslo ministerija Rusijos Federacija Novosibirsko valstybinis universiteto fakulteto fakulteto R. K. Belleeva Ryadov Fourier pavyzdžiais ir Užduotys Tutorial Novosibirsk 211

2 UDC BBK BL161 B44 B44 BELLEEVA R. K. Fourier eilutės pavyzdžių ir užduočių: Tutorial / Novosib. Valstybė un-t. Novosibirskas, p. ISBN tyrimo vadove pateikiama pagrindinė informacija apie "Fourier" gretas, kiekvienai studijuotai temai yra pavyzdžių. Furjė metodo naudojimo pavyzdys yra išsamiai išmontuotas sprendžiant styginių skersinių virpesių problemą. Pateikiama iliustracinė medžiaga. Yra užduočių nepriklausomam sprendimui. Skirta NSU fizinio fakulteto studentams ir mokytojams. Atspausdintas NSU fizinio fakulteto metodikos komisijos sprendimu. Recenzentas dr. Fiz.-Mat. Mokslas V. A. Aleksandrovo pašalpa parengta kaip Niu-NSU programos plėtros programos įgyvendinimo dalis. Isbn C Novosibirski valstijos universitetas, 211 C BELLEEVA R. K., 211

3 1. 2π-periodinės funkcijos skilimas į "Fourier" serijos apibrėžimą. Netoli Fourier funkcija F (x) yra vadinama funkcine serija A 2 + ("Cosnx + Bn Sin NX"), (1) kai, BN koeficientai apskaičiuojami naudojant formules: an \u003d 1 π bn \u003d 1 π f (x) cosnxdx, n \u003d, 1, ..., 2) f (x) sin nxdx, n \u003d 1, 2, .... (3) Formulės (2) (3) vadinami Euler Fourier formulėmis. Tai, kad F (x) funkcijos atitinka Furjė seriją (1) yra įrašomos kaip F formulė F (X) A 2 + (COSNX + BN SIN NX) (4) ir sakoma, kad dešinė pusė (4) formulės yra oficialus "Fourier" funkcija f (x). Kitaip tariant, formulė (4) reiškia tik tai, kad koeficientai A N, B n yra rasti formulės (2), (3). 3.

4 Apibrėžimas. 2π-periodinė funkcija F (x) yra vadinama sklandžiu, jei intervale [, π] yra baigtinis taškų skaičius \u003d x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 pav. 1. Funkcijos funkcija F (x) Apskaičiuokite "Fourier" koeficientus a \u003d 1 π f (x) dx \u003d 1 π x 2 2 π \u003d π, an \u003d 1 π f (x) cosnxdx \u003d 2 π \u003d 2 () x sin nx cos NX + π nn 2 \u003d 2 π (1) n 1 n 2 \u003d bn \u003d 1 π π \u003d 2 π f (x) cosnxdx \u003d cos nx cos n 2 \u003d 4 πn2, su n nelyginiu, su N lyg, f (x ) Sin nxdx \u003d, nes funkcija f (x) yra netgi. Rašome formalią Furjė seriją f (x): f (x) π 2 4 π k \u003d 5 cos (2K + 1) x (2K + 1) 2.

6 Sužinokite, ar F (x) funkcija yra lygi sklandžiai. Kadangi jis yra nepertraukiamas, apskaičiuojame tik ribas (6) ribų taškuose x \u003d ± π ir pertraukos x \u003d: ir f (π (h) f (π) π π lim \u003d LIM H + HH + H \u003d 1, F (+ h) f (+) + h () LIM \u003d LIM H + HH + HF (+ h) f (+) + H LIM \u003d LIM \u003d 1, H + HH + H \u003d 1, f (h) f () h () LIM \u003d LIM \u003d 1. H + HH + H ribos egzistuoja ir yra baigtinis, todėl gabalas gabalas sklandžiai. Pasak dabartinės konvergencijos, jos "Fourier" serijos konverguojančios į numerį f (x) kiekviename taške, ty f (x) \u003d π 2 4 π k \u003d cos (2k + 1) + x (2K + 1) 2 \u003d \u003d π 2 4 (COSX + 19 π COS 3X) COS 5x (7) Fig. 2, 3 rodo iš dalinių sumų, kurių Furlier serijos s (x), kur s n (x) \u003d 2 + (AK coskx + bk sin kx), k \u003d 1 į funkciją f (x ) intervale [, π]. 6.

7 pav. 2. Funkcijos f (x) grafikas su dalinėmis sumomis S (x) \u003d A 2 ir S 1 (x) \u003d A 2 + A 1 COS X x yra ant jo. 3. F priedas F (X) funkcija su daline sumą S 99 (x) \u003d a 2 + a 1 cos x + + a 99 cos 99x 7

8 (7) x \u003d mes gauname: \u003d π 2 4 π k \u003d 1 (2K + 1) 2, iš kur mes randame skaitmeninės serijos sumą: \u003d π2 8. Žinant šią eilutę, tai yra Lengva rasti tokią sumą: S \u003d () s \u003d () \u003d π, todėl s \u003d π2 6, ty 1 n \u003d šios garsiosios eilės sumos pirmą kartą surado Leonard Euler. Jis dažnai randamas matematinėje analizėje ir jos taikymuose. 2. Pavyzdys 2. Nubraižykite tvarkaraštį, mes randame Fourier serijos iš tam tikros formulės f (x) \u003d x už X funkciją< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 pav. 4. F (X) Funkcija F (x) funkcija intervale nuolat diferencijuojama (π). Taškuose x \u003d ± π, jis turi ribotą ribą (5): f () \u003d, f (π) \u003d π. Be to, yra galutinių ribų (6): f (+ h) f (+) lim \u003d 1 ir h + hf (π h) f (π +) lim \u003d 1. h + h reiškia f (x) gabalas sklandžiai funkcija. Kadangi F (x) funkcija yra keista, tada n \u003d. BN koeficientai Rasti integraciją į dalis: BN \u003d 1 π f (x) sin πnxdx \u003d 1 [x cosnx π πn + 1 n \u003d 1 πn [(1) n π + (1) n π] \u003d 2 (1) n + vienas. N padaryti formalią Furjė serijos funkcijas 2 (1) n + 1 f (x) sin nx. N 9 cosnxdx] \u003d

10 Pagal teoremo ant dabartinės konvergencijos dalywewe slide 2π-periodinė funkcija, Furjė serija f (x) yra susiliejęs į sumą: 2 (1) n + 1 sin nx \u003d n f (x) \u003d x, jei π π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 pav. 6. Funkcijos f (x) grafikas su daline S 2 (x) sumontuota ant jo). 7. F priedas (X) Funkcija su daline suma s 3 (x) 11 yra ant jo.

12 pav. 8. Funkcijos f (x) grafikas su daline S 99 (x) sumontuota ant jo) Naudokite gautą Furjė seriją rasti dviejų skaitmeninių eilučių sumas. Įdėkite (8) x \u003d π / 2. Tada 2 () + ... \u003d π 2, arba \u003d n \u003d (1) n 2n + 1 \u003d π 4. Mes lengvai radome žinomos Leibito eilutės sumą. Įdėjimas į (8) x \u003d π / 3, mes rasime () + ... \u003d π 2 3, arba (1+ 1) () (k) 3π + ... \u003d 3k

13 pavyzdys 3. Nubraižykite tvarkaraštį, mes randame Fourier serijos funkciją F (x) \u003d Sin X, darant prielaidą, kad jis turi 2π, ir 1 apskaičiuoti skaitinės serijos 4n 2 sumą 1. tirpalas. Grafiko funkcija f (x) rodoma Fig. 9. Akivaizdu, kad F (x) \u003d Sin X yra nuolatinė netgi funkcija su π. Bet 2π taip pat yra funkcija F (x) funkcija. Fig. 9. Funkcijos funkcija F (x) Apskaičiuokite "Fourier" koeficientus. Visi b n \u003d nes funkcija yra net. Pasinaudojant trigonometriniais formulėmis Apskaičiuokite n 1: an \u003d 1 π \u003d 1 π sin x cosnxdx \u003d 2 π sin x cosnxdx \u003d (Sin (1 + N) x Sin (1 n) x) dx \u003d 1 () π cos (1 + N) x cos (1 n) x + \u003d 2 () 1 + (1) n \u003d π 1 + n 1 n π 1 n 2 (4 1, jei n \u003d 2k, \u003d π n 2 1, jei N \u003d 2k.

14 Šis skaičiavimas neleidžia mums rasti koeficiento A 1, nes su N \u003d 1, vardiklio adresai iki nulio. Todėl apskaičiuojame koeficientą 1 tiesiogiai: 1 \u003d 1 π sin x cosxdx \u003d. Kadangi f (x) yra nuolat diferencijuojamos (,) ir (, π) ir taškuose kπ, (k sveikasis skaičius), yra galutinių ribų (5) ir (6), tada fourier diapazonas funkcija konverguojasi į jį Kiekvienas taškas: \u003d 2 π 4 π sinx \u003d 2 π 4 π cos 2nx 4n 2 1 \u003d (1 1 1 cos 2x cos 4x + 1) COS 6x Funkcijos fonto (x) dalinės sumos pobūdis. rodomas "Fourier" asortimentas. (9) Fig. 1. F priedas F (X) funkcija su daline suma S (x) 14 ant jo

15 ryžių 11. Funkcijos f (x) grafikas su daline suma) su daline sumą s 1 (x) pav. 12. Funkcijos f (x) grafikas su daline sumomis S 2 (x) ant jo). 13. FUNKCIJOS FUNKCIJA F (x) su daline suma S 99 (x) 15 yra ant jo

16 1 Apskaičiuokite skaitmeninės serijos sumą. Už tai, 4n 2 1 įdėti į (9) x \u003d. Tada cosnx \u003d 1 visiems n \u003d 1, 2, ... ir todėl 2 π 4 π 1 4n 2 1 \u003d. 1 4n 2 1 \u003d 1 \u003d 1 2. PAVYZDYS 4. ĮSIPAREIGOJO, KAD SUKURTI SLOOTY FOUND FUNKCIJA F (x) atitinka f (x π) \u003d f (x) visą X (t. I.E. yra π-periodinis), \\ t Tada 2n 1 \u003d b 2n 1 \u003d visiems N 1, ir atvirkščiai, jei 2n 1 \u003d B 2N 1 \u003d visiems n 1, tada f (x) π-periodiškai. Sprendimas. Leiskite funkcijai f (x) būti π-periodiškai. Apskaičiuokite savo "Fourier" koeficientus 2n 1 ir b 2n 1: \u003d 1 π (a 2n 1 \u003d 1 π f (x) cos (2n 1) xdx + f (x) cos (2n 1) xdx \u003d) f (x) cos (2n 1) xdx. Pirmajame integrale pakeisime kintamąjį x \u003d t π: f (x) cos (2n 1) xdx \u003d f (t π) cos (2n 1) (t + π) dt. šešiolika metų

17 Atsižvelgiant tokiu būdu, kad cos (2n 1) (t + π) \u003d cos (2n 1) t ir f (t π) \u003d f (t), mes gauname: a 2n 1 \u003d 1 π (f (x) cos ( 2n 1) x dx +) f (x) cos (2n 1) x dx \u003d. Panašiai įrodyta, kad B 2N 1 \u003d. Priešingai, leiskite 2n 1 \u003d B 2N 1 \u003d. Kadangi Funkcija f (x) yra nuolatinis, tada teorijos dėl funkcijos Atstovai tuo savo kitą Fourier, mes tada F (x π) \u003d \u003d f (x) \u003d (a 2n cos 2nx + b 2n Sin 2nx). (A2N COS 2N (x π) + B 2N SIN 2N (x π)) \u003d (A2N COS 2NX + B 2N SIN 2NX) \u003d f (x), o tai reiškia, kad f (x) yra π-periodinė funkcija. Pavyzdys 5. Mes įrodome, kad jei "Pievewise Sklandus FF" (x) atitinka sąlygą f (x) \u003d f (x) visiems x, tada a \u003d ir a 2n \u003d b 2N \u003d visiems N 1, ir atvirkščiai, Jei a \u003d a 2n \u003d b 2n \u003d, tada f (x π) \u003d f (x) visiems x. Sprendimas. Leiskite funkcijai f (x) atitinka f (x π) \u003d f (x) būklę. Apskaičiuokite savo "Fourier" koeficientus: 17

18 \u003d 1 π (a n \u003d 1 π f (x) cos nxdx + f (x) cosnxdx \u003d) f (x) cosnxdx. Pirmajame integrale pakeisime kintamąjį x \u003d t π. Tada f (x) cosnxdx \u003d f (t π) cosn (t π) dt. Tokiu būdu, kad cos n (t π) \u003d (1) n cosnt ir f (t) \u003d f (t), mes gauname: an \u003d 1 π ((1) n) f (t) cosnt dt \u003d jei N lygus, \u003d 2 π f (t) cos nt dt, jei n yra keista. π Taip pat įrodyta, kad B 2N \u003d. Priešingai, tegul a \u003d a 2n \u003d b 2n \u003d, visiems n 1. Kadangi funkcija f (x) yra nuolatinė, tada atstovaujamumo teorema, lygybė f (x) \u003d (a 2n 1 cos (x x cos (x ) \u003d (2n 1 cos (2n 1) x + B 2N 1 nuodėmė (2n 1) x). aštuoniolika

19 Tada \u003d f (x π) \u003d \u003d \u003d f (x). 6 pavyzdys Mes studijuojame, kaip tęsti F (x) funkciją, integruota į intervalą [, π / 2] į [, π] intervalą, kad jo "Fourier" serija mano: 2n 1 cos (2n 1) x. (1) Sprendimas. Leiskite funkcijų grafikui peržiūrėti Fig. 14. Kadangi per numerį (1) a \u003d a \u003d a \u003d 2n \u003d b 2n \u003d visiems N, tada nuo 5 pavyzdžio, iš dalies, kad funkcija f (x) turi atitikti lygybę f (x π) \u003d f (x) visiems x. Šis stebėjimas suteikia galimybę tęsti f (x) funkciją į intervalą [, / 2]: F (x) \u003d f (x + π), Fig. 15. Iš to, kad eilėje (1) yra tik kosinimai, darome išvadą, kad tęstinė funkcija f (x) turėtų būti net (t. Y. Jos tvarkaraštis turėtų būti simetriškas dėl OY ašies), ryžių

20 pav. 14. Funkcijos grafikas f (x) pav. 15. Tvarkaraštis Funkcijos tęsinys F (x) intervalui [, / 2] 2

21 Taigi, norima funkcija yra vertinama Fig. 16. Pav. 16. Prašo tęsti funkciją F (x) intervalui [, π] sumaišyti, mes darome išvadą, kad funkcija turėtų būti tęsiama taip: f (x) \u003d f (x), f (π x) \u003d f ( x), tai yra, intervalas [π / 2, π], funkcijos f (x) grafikas yra centralizuotai simetriškas taškui (π / 2) ir intervalui [, π], jo grafiką yra simetriškas dėl Oy ašies. 21.

22 pavyzdžių apibendrinimas 3 6 Leiskite L\u003e. Apsvarstykite dvi sąlygas: a) f (L x) \u003d f (x); b) f (l + x) \u003d f (x), x [, l / 2]. Geometriniu požiūriu, a) reiškia, kad grafiko funkcija f (x) yra simetriška vertikaliam tiesiogiai x \u003d l / 2, ir būklė (b), kad f (x) grafikas yra centralizuotas simetriškas su tašku (l / 2;) ant ašies abscissa. Tada yra šie teiginiai. 2) Jei F (x) funkcija yra lygi (b), tada b 1 \u003d b 2 \u003d b 3 \u003d ... \u003d, a \u003d a2 \u003d a 4 \u003d ... \u003d; 3) Jei funkcija f (x) yra nelyginė ir būklė (a) yra patenkinta, tada a \u003d a 1 \u003d a2 \u003d ... \u003d, b2 \u003d b 4 \u003d b 6 \u003d ... \u003d; 4) Jei funkcija f (x) yra nelyginė ir būklė (b) yra įvykdyta, tada a \u003d a 1 \u003d a2 \u003d ... \u003d, b 1 \u003d b 3 \u003d b 5 \u003d ... \u003d. Užduotys užduotys 1 7 Nupieškite grafikus ir suraskite Furjė seriją funkcijoms (darant prielaidą, kad jie turi 2π laikotarpį:, jei< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 (1, jei / 2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. Intervale nurodytos funkcijos skaidymas [π], tik sinusas arba tik "Cosine". Leiskite funkcijai f nustatyta intervale [, π]. Nenaudokite jį šioje spragoje Furjė eilėje, pirmiausia tęsime f į intervalą [, π] atsitiktinai, tada naudokite Euler Fourier formules. Arbitraškumas tęsiant funkciją lemia tai, kad už tą pačią funkciją F: [, π] R mes galime gauti skirtingas Fourier eilutes. Bet jūs galite naudoti šį savavališkumą gauti skilimą tik sin sines arba tik pagal kosiną: pirmuoju atveju pakanka tęsti f keista, ir antra. Sprendimas algoritmas 1. Tęskite funkciją į nelyginį (lygų) kelią (,) ir tada periodiškai su 2π tęsti funkciją ant visos ašies. 2. Apskaičiuokite "Fourier" koeficientus. 3. Padarykite Furjė seriją f (x). 4. Patikrinkite eilutės konvergencijos sąlygas. 5. Nurodykite funkciją, su kuria ši serija susilieja. 7 pavyzdys. Skleiskite funkciją f (x) \u003d cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 pav. 17. Tęstinės funkcijos tvarkaraštis yra akivaizdus, \u200b\u200bkad F (x) funkcija yra lygi. Apskaičiuokite "Fourier" koeficientus: n \u003d visiems n, nes funkcija f (x) yra keista. Jei n 1, tada bn \u003d 2 π f (x) sin πnxdx \u003d 2 π cosx sin nxdx \u003d 2 π dx \u003d 2 π cos (n + 1) x cos (n 1) x + \u003d π n + 1 n 1 \u003d 1 (1) n (1) n 1 1 \u003d π n + 1 n 1 \u003d 1, jei n \u003d 2 k + 1, (1) n + 1 (n 1) + (n + 1) \u003d π (n +) 1) (n 1) 2 2n, jei n \u003d 2k. π N 2 1 N \u003d 1 Ankstesniuose skaičiavimuose, vardiklis reiškia nulį, todėl koeficientas B 1 apskaičiuojamas tiesiogiai- 25

26: B 1 \u003d 2 π Cosx Sin Xdx \u003d. Mes sudarysime Furjė funkcijos F (x): F (x) 8 π k \u003d 1 k 4k 2 1 Sin 2kx. Kadangi Funkcija f (x) yra lygus sklandžiai, tada pagal detektyvo konvergencijos teoremą, Furjė spektrą f (x) funkcija konverguojančia sumą: COSX, jei π π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 pav. 18. Funkcijos f (x) grafikas su daline sumomis s 1 (x) yra ant jo. 19. F priedas (X) Funkcija su daline S 2 (x) 27 sumomis

28 pav. 2. Funkcijos f (x) grafikas su daline S 3 (x) sumomis, kurios ant jo yra) Fig. 21 rodo funkcijos f (x) grafikus ir dalinę sumą S 99 (x). Fig. 21. F priedas F (X) funkcija su daline suma S 99 (x) 28 supjaustyta ant jo

29 pavyzdys 8. Numatykite funkciją F (x) \u003d E kirvis, A\u003e, X [, π], iš eilės iš eilės tik Cosine. Sprendimas. Mes tęsiame funkciją vienodai () (ty, kad lygybė f (x) \u003d f (x) buvo atlikta visiems x (, π)), o po to periodiškai su 2π vienam skaitine ašimi . Mes gauname F (x) funkciją, kurio grafikas pateikiamas Fig. 22. Funkcija f (x) taškuose. 22. Toliau Funkcijos f (x) x \u003d kπ, k yra sveikas skaičius, turi lapę. Apskaičiuokite "Fourier" koeficientus: b n \u003d, nes f (x) yra netgi. Integruojant dalis mes gauname 29

30 an \u003d 2 π a \u003d 2 π \u003d 2 cosnxd (ex) \u003d 2 πa ex dx \u003d 2 π a (eaπ 1), f (x) cos πnxdx \u003d 2 π πa eax cosnx \u003d 2 πa (eaπ cosnπ 1 ) + 2n πa 2 π ex cos nxdx \u003d + 2n e ax sin nxdx \u003d πa sin nxde ax \u003d 2 πa (eaπ cos n π 1) + 2n π sin nx π a 2eax 2n2 e ax cos nxdx \u003d 2 π a 2 π A (EAπ COS N π 1) N2 AA N. 2, a n \u003d 2a e aπ cos n π 1. π A 2 + N 2 Nuo f (x) yra nepertraukiamas, tada pagal dabartinės konvergencijos srovę, jo Fourier eilutės konverguojančios iki F (x). Taigi, visiems x [, π], mes turime f (x) \u003d 1 π a (EAN 1) + 2A π k \u003d 1 e Aπ (1) k 1 A 2 + K 2 coskx (x π). Ryžiai parodo laipsniškai suderinimą dalinių sumų Furjė serijos į tam tikrą sprogimo funkciją. 3.

31 pav. 23. Funkcijų grafikai f (x) ir s (x) pav. 24. Funkcijų grafikai F (x) ir s 1 (x) pav. 25. Funkcijų grafikai f (x) ir s2 (x) pav. 26. Funkcijų grafikai F (x) ir s 3 (x) 31

32 pav. 27. Funkcijų grafikai F (x) ir S 4 (x) pav. 28. FUNKCIJŲ DIHS F (x) ir S 99 (x) Užduotys 9. Naršykite funkciją F (x) \u003d cos x, x π, "Fourier" eilutėje tik "Cosine". 1. Naršykite funkciją f (x) \u003d e ax, a\u003e, x π, fourier serijos tik sinuso. 11. Naršykite F (x) \u003d x 2, x π fourier serijos tik sinusuose. 12. Skleiskite F (x) \u003d Sin Ax, x π, Furjė serijos tik Cosine. 13. Skleiskite funkciją f (x) \u003d x sin x, x π, "Fourier" serijoje tik sinuse. Atsakymai 9. cosx \u003d cosx. 1. E AX \u003d 2 [1 (1) k e aπ] k sin kx. π A 2 + k2 k \u003d 1 11. x 2 2 [π 2 (1) n 1 π n + 2] N 3 ((1) N 1) Sin NX. 32.

33 12. Jei A nėra sveikas skaičius, tada sin AX \u003d 1 COSAπ (1 + 2A COS 2NX) + π A 2 (2N) 2 + 2A 1 + COSAπ COS (2N 1) x π A 2 (2N 1) 2 ; Jei a \u003d 2m yra lygus skaičius, tada nuodėmė 2mx \u003d 8m cos (2n 1) x π (2m) 2 (2n 1) 2; Jei a \u003d 2m 1 yra teigiamas nelyginis skaičius, tada nuodėmė (2m 1) x \u003d 2 (cos 2nx) 1 + 2 (2m 1). π (2m 1) 2 (2n) π 16 N Sin X Sin 2nx. 2 π (4n 2 1) 2 3. Furjė serijos funkcijų su savavališku laikotarpiu Tarkime, kad funkcija f (x) yra nustatyta intervale [l, l], l\u003e. Padarydami pakeitimą x \u003d ly, y π, gauname funkciją g (y) \u003d f (ly / π), nustatytas spragoje π [, π]. Ši funkcija g (y) atitinka (formalią) "Fourier" seriją () ly f \u003d g (y) a π 2 + ("cosny + bn sin ny"), kurių koeficientai yra pagal Euler Fourier formules: an \u003d 1 π g (y) cosny dy \u003d 1 π f (ly π) cos ny dy, n \u003d, 1, 2, ..., 33

34 bn \u003d 1 π g (y) sinny dy \u003d 1 π f () ly sin ny dy, n \u003d 1, 2, .... π grįžta į seną kintamąjį, t.y. tikėjimas rašytinėmis formulėmis y \u003d πx / l , Mes gauname funt f (x) trigonometrinių serijų kelis modifikuotus tipas: kur f (x) a 2 + an \u003d 1 lbn \u003d 1 lllll (a cos πnx lf (x) cos πnx lf (x) sin πnx l + bn Sin πnx), (11) l dx, n \u003d, 1, 2, ..., 12) dx, n \u003d 1, 2, .... (13) Sakoma, kad formulės (11) (13) yra nurodytas skilimas į Fourier serijos funkcijas su savavališku laikotarpiu. 9 pavyzdys. Mes rasime "Fourier" serijos nurodytą intervalo (L, L) išraiškos (a, jei l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 A \u003d 1 llf (x) dx \u003d 1 l a dx + 1 ll b dx \u003d a + b, llan \u003d 1 lllf (x) cos πnx l dx \u003d 1 l \u003d 1 ll a cos πnx l \u003d a + b π nlbn \u003d 1 l dx + 1 ll b cos πnx l sin πn \u003d, jei n, ll sin πnx lf (x) Sin πnx l dx + 1 ll dx \u003d b sin πnx l \u003d ba (1 cosπn). πn bus iš eilės fourier funkcija f (x): f (x) a + b π (b a nuo cosπn \u003d (1) n, tada n dx \u003d dx \u003d (1 cosπn) nuodėmės πnx). l už n \u003d 2k mes gauname b n \u003d b 2k \u003d, su n \u003d 2K 1 b n \u003d b 1 \u003d 35 2 (B a) π (2k 1).

36 iš čia F (x) A + B (BA) π (Sin πx + 1 3πx Sin + 1 5πx Sin + ... L 3 L 5 l Pagal Degenerate konvergencijos teoremą, Furjė serija F (X) yra susieta su suma, jei L.< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 pav. 29. Funkcijos f (x) diagrama su diagramomis, su kuriomis susiduria harmonika s (x) \u003d A 2 ir S 1 (x) \u003d B 1 Sinx. Dėl trijų didesnių harmonikų s 3 (x) \u003d B 3 sin 3πx, S L 5 (x) \u003d B 5 sin 5πx l ir s 7 (x) \u003d B 7 sin 7πx perkelta vertikali iki L 37

38 pav. 3. Funkcijos f (x) grafikas su daline S 99 (x) suma yra ant jo. 31. Fragmentas. 3 kitoje skalėje 38

39 Užduotys užduotys, kad būtų išstumtos nurodytos funkcijos nurodytais intervalais. 14. F (x) \u003d x 1, (1, 1). 15. F (x) \u003d CH2X, (2, 2] F (x) \u003d x (1 x), (1, 1]. 17. F (x) \u003d cos π x, [1, 1] f (x ) \u003d nuodėmė π x, (1, 1). (2 1, jei 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18. F (x) \u003d 8 (1) n n sin nπx. π 1 4n (1) N 2N + 1 cos πx. π 2n πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (L 22. a) f (x) \u003d al 4 2) 1 (4n 2) πx cos, π 2 (2n 1) 2 L B) f (x) \u003d 4al (1) n 1 (2n 1) πx sin. π 2 (2n 1) 2 L 23. a) f (x) \u003d (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x ... b) f ( x) \u003d 4 (nuodėmė π π 2 2 x 1 3 sin 3π) + 2 2 x (sin π π 2 x cos 2π) 2 x sudėtinga fourier skilimo f forma (x) \u003d CNE INX, kur CN \u003d 1 2π f (x) e inx dx, n \u003d ± 1, ± 2, ... vadinama sudėtinga fourier serijos forma. Funkcija suskaido į sudėtingą "Furtier" seriją atliekant tas pačias sąlygas, pagal kurias jis susilpnina į "Fourier Real" serijas. Keturi

41 pavyzdys 1. Raskite Fourier seriją sudėtingoje forpuso formoje F (X) \u003d E kirvis, intervale [, π), kur yra realus skaičius. Sprendimas. Apskaičiuokite koeficientus: \u003d C n \u003d 1 2π f (x) e inx dx \u003d 1 2π e (a in) x dx \u003d 1 ((1) n e aπ (1) n e aπ) \u003d (1) n sh aπ. 2π (a in) π (a Inv.) Sudėtinga Furlier serija F yra f (x) sh aπ π n \u003d (1) n a einx. Jis yra įsitikinęs, kad F (x) funkcija yra lygi: intervale (, π) jis nuolat diferencijuojamas, o taškuose x \u003d ± π egzistuoja baigtinių ribų (5), (6) LIM H + EA ( + H) \u003d E Aπ, Lim H + Ea (π h) \u003d e Aπ, ea (+ h) Ea (+) Lim H + H \u003d AE Aπ EA (π h) ea (π), Lim H + H \u003d Ae aπ. Todėl funkcija f (x) yra atstovaujanti fourier sh aπ π n \u003d (1) n a einx, kuris susilieja su sumos: (s (x) \u003d kirvis, jei π π< x < π, ch a, если x = ±π. 41

42 pavyzdys. Mes rasime "Fourier" seriją sudėtingoje ir tikroje funkcijos formoje F (X) \u003d 1 A 2 1 2A COSX + A2, kur a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 Prisiminkite, kad begalinės geometrinės progresavimo suma su vardikliu Q (Q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 Dabar mes rasime "Fourier" seriją tikroje formoje. Norėdami tai padaryti, suskirstėme terminus su N ir N N ir N: a n e inx + a n e inx \u003d 2a neinx + e inx, nes c \u003d 1, tada 2 \u003d 2a n cos nx. f (x) \u003d 1 a 2 1 2a cosx + a \u003d a n cosnx. 2 Tai yra "Fourier" serija tikroje F (X) funkcijoje. Taigi, be vieno integralo, mes radome keletą Furjė funkcijų. Tuo pačiu metu apskaičiuojant sudėtingą integralą, priklausomai nuo parametro cos nxdx 1 2a cosx + a \u003d 2 π 2 1 a2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 A (ZZ 1) F (x) \u003d 2i (1 a (ZZ 1) + a 2) \u003d I 2 + I (A + A 1) Z 2 2 (ZA) (ZA 1) \u003d \u003d i 2 + I () 2 za + a 1. Za 1 Kiekviena iš paprastų frakcijų suskaido pagal geometrinio progresavimo formulę: + aza \u003d a 1 z 1 a \u003d aanzzn, n \u003d za \u003d az \u003d anz n. n \u003d tai įmanoma, nes az \u003d a / z \u003d a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >arba, trumpas, C n \u003d 1 2i n sgnn. Taigi, Fourier serijos išsamioje formoje. Suderino su numeriais su numeriais N ir N mes gauname "Fourier" funkcijų seriją realioje formoje: \u003d F (x) \u003d + Sin x 1 2a cosx + a + 2 (1 2i e inx 1 2i e inx n \u003d +) \u003d CNE INX \u003d SIN NX. Mes vėl sugebėjome apskaičiuoti šiuos sudėtingus integrumą: Sin X Sin NXDX 1 2A Cosx + A 2 \u003d π 1. (16) 45

46 Užduotys 24. Naudojant (15), apskaičiuoti COS NXDX 1 2A COSX + A 2 integralą realiam A, A,\u003e Naudojant (16), apskaičiuoti SIN X SIN NXDX integralą realiam a, a\u003e a cosx + a2 Užduotys, surasti eilutes Fourning išsamią formą funkcijų. 26. f (x) \u003d sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Lyapunovo teoremo (Lyapunov lygybės) lygybė. Leiskite funkcijai f: [, π] r tai yra toks, kad F2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n \u003d 2 π f (x) cosnxdx \u003d 2 π a cos nxdx \u003d 2 sin na πn. Todėl "Lyapunov" už funkciją f (x) yra forma: 2 a 2 π + 4 sin 2 na \u003d 2a 2 π 2 n 2 π. Nuo paskutinio lygybės π mes randame nuodėmę 2 NA N 2 \u003d a (π a) 2, darant prielaidą, kad a \u003d π 2, mes gauname sin2 na \u003d 1 n \u003d 2k 1 ir sin 2 na \u003d n \u003d 2k. Todėl k \u003d 1 1 (2k 1) 2 \u003d \u003d π2 8. 14 pavyzdys. Mes parašysime Lapunov lygybę f (x) \u003d x cosx, x [, π], ir mes surasime sumą Skaitmeninė eilutė (4n 2 + 1) 2 (4n 2 1) 4. 1 π tirpalas. Tiesioginiai skaičiavimai suteikia \u003d π π f 2 (x) dx \u003d 1 π x 2 cos 2 xdx \u003d 1 π x sin 2xdx \u003d π π x cos x \u003d π x 21 + cos 2x dx \u003d 2 π 1 4π cos 2xdx \u003d

49 Kadangi f (x) yra net veikimas, tada visiems n mes turime bn \u003d, an \u003d 2 π \u003d 1 π 1 \u003d π (n + 1) \u003d f (x) cosnxdx \u003d 2 π 1 cos (n + 1 ) x π (n + 1) 2 x cosxcosnxdx \u003d x (cos (n + 1) x + cos (n 1) x) dx \u003d 1 π sin (n + 1) xdx sin (n 1) xdx \u003d π (n 1) π π 1 + cos (n 1) x \u003d π (n 1) 2 1 (\u003d (1) (n + 1) 1) 1 (+ (1) (n + 1) 1) \u003d π (n + 1) 2 π (n 1) 2 () \u003d (1) (n + 1) 1 1 π (n + 1) + 1 \u003d 2 (n 1) 2 \u003d 2 (1) (n + 1) 1 nk π π (N 2 1) \u003d π (4k 2 1) 2, jei n \u003d 2k, 2, jei n \u003d 2K + 1. koeficientas A 1 turi būti apskaičiuojamas atskirai, nes bendroje N \u003d 1 formulėje yra denomoteris nulio. \u003d 1 π a 1 \u003d 2 π f (x) cosxdx \u003d 2 π x (1 + cos 2x) dx \u003d π 2 1 2π 49 x cos 2 xdx \u003d sin 2xdx \u003d π 2.

50 Taigi, "Lyapunov" funkcijos lygybė f (x) turi formą: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) \u003d π, iš kur randame skaitinės eilutės sumą (4n 2 2 + 1) 2 (4n 2 1) \u003d π π užduotys 32. Parašykite "Lyapunov" lygybę funkcijai (xf (x) \u003d 2 πx, jei x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) \u003d π sin 2απ 2απ \u003d 2sin2 απ α 2 π 2 atsakymai + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; Sin 2απ 1 2απ \u003d απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. F (x) g (x) DX \u003d CNDN, kur CN Fourier koeficientas 2π Funkcijos F (x) ir DN Fullier koeficientas Funkcijos g (x). 6. Furjė serijos diferenciacija Leiskite F: R r nuolat diferencijuoti 2π periodinę funkciją. Jos Furjė serija turi formą: F (x) \u003d a 2 + (a n cos nx + b n sin nx). Šios funkcijos darinys F (x) bus tęstinis ir 2π periodinė funkcija, kuriai galima parašyti Furjė formalią diapazoną: F (x) A 2 + ("Cos NX + Bn Sin NX"), kur a, an, BN, N \u003d 1, 2, ... Furjė koeficientai f (x). 51.

52 teorema (apie nužudytą Furjė serijos diferenciaciją). Su pirmiau pateiktomis prielaidomis, lygybė A \u003d, n \u003d NB N, B n \u003d na n, n 1. 1 pavyzdys. Laikykitės sklandaus funkcijos F (x) intervalu [π]. Mes įrodome, kad atliekant sąlygą f (x) dx \u003d, yra nelygybė 2 dx 2 dx, vadinama stiklo nelygybe ir įsitikinkite, kad jame esanti lygybė atliekama tik f (x) formos funkcijoms \u003d a Cosx. Kitaip tariant, Steklov nelygybė suteikia sąlygas, atliekant darinio (RMS) mažumą, seka funkcijos mažumą (vidurkyje - vidurkyje). Sprendimas. Mes tęsime funkciją f (x) intervalui [,] tolygiai. Žymi tolesnį to paties simbolio f (x) funkciją. Tada tęstinė funkcija bus nuolatinė ir dalijasi segmente [, π]. Kadangi funkcija f (x) yra nepertraukiama, tada f2 (x) yra nuolatinis segmente ir 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Kadangi tęstinė funkcija yra net, tada b n \u003d, a \u003d pagal būklę. Todėl Lyapunovo lygybė trunka 1 π 2 dx \u003d a 2 π n. (17) yra įsitikinęs, kad f (x) yra sudarytas "Furjier" serijos "Furjier" serijos diferenciacija, ty a \u003d, an \u003d nb n, bn \u003d na n, n 1. leiskite Išvestinė f (x) pertraukos yra x 1, x 2, ..., x n intervale [, π]. Reiškia x \u003d, x n + 1 \u003d π. Mes padalijame integracijos intervalą [, π] N +1 tarpo (x, x 1), ..., (x n, x n + 1), kurių kiekvienas yra f (x), nuolat diferencijuojamas. Tada, naudojant integruoto priedo nuosavybę ir tada integruoti į dalis, mes gauname: BN \u003d 1 π \u003d 1 π \u003d 1 π f (x) sin nxdx \u003d 1 π nf (x) sin nx j \u003d nf ( x) sin nx j \u003d xj + 1 xjx j + 1 xjnn π nj \u003d xj + 1 x jx j + 1 xjf (x) sin nxdx \u003d f (x) cosnxdx \u003d f (x) cosnxdx \u003d \u003d 1 π [(f x 1) nuodėmės nx 1 f (x) sin nx) + + (f (x 2) sinnx 2 f (x 1) sin nx 1)

54 + (F (x n + 1) sin nx n + 1 f (x n) sin nx n)]] na n \u003d 1 π na n \u003d \u003d 1 π na n \u003d na n. X J + 1 A \u003d 1 f (x) dx \u003d 1 n f (x) dx \u003d π π j \u003d xj \u003d 1 n x j + 1 f (x) π \u003d 1 (f (π (π) f ()) \u003d. X J π j \u003d paskutinė lygybė vyksta dėl to, kad F (x) funkcija tęsiama tolygiai, todėl f (π) \u003d f (). Panašiai mes gauname n \u003d nb n. Mes parodėme, kad "Fourier" serijos "Fourier" serijos renovacijos diferencijavimas už nuolatinį išlyginamą 2π periodinę funkciją, iš kurios darinys, kurių intervalas [, π] patiria pirmojo tipo pertraukas, yra teisinga. Taip f (x) a 2 + (cosnx + bn sin nx) \u003d (na n) sin nx, kaip a \u003d, an \u003d nb n \u003d, bn \u003d na n, n \u003d 1, 2, nuo to laiko 2 DX.< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Kadangi kiekvienas eilutės narys (18) yra didesnis arba lygus atitinkamam eilutės nariui (17), tada 2 DX 2 DX. Prisimindami, kad f (x) yra netgi pradinės funkcijos tęsinys, turime 2 dx 2 dx. Kas įrodo Steklov lygybę. Dabar mes tiriame, kokios funkcijos stoklovo, yra lygybė. Jei bent už N 2, koeficientas n skiriasi nuo nulio, tada 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 Užduotys 37. Laikykitės sklandaus funkcijos f (x) intervalu [π]. Įrodyti, kad atliekant sąlygą f () \u003d f (π) \u003d, yra 2 DX 2 DX nelygybė, taip pat vadinama stiklo įranga, ir įsitikinkite, kad lygybė jame vyksta tik f (x) formos funkcijoms funkcijoms \u003d b sin x. 38. Leiskite FUNKCIJA F yra nuolatiniai intervalui [, π] ir jame yra (išskyrus paskutinį taškų skaičių) Išvestinė f (x) integruota su kvadratą. Įrodyti, kad jei sąlygos f () \u003d f (π) ir f (x) dx \u003d yra įvykdytos, tada yra nelygybė 2 dx 2 dx, vadinamą "Virginger" nelygybę, o lygybė yra tik funkcijoms f (x) \u003d a cosx + b sin x. 56.

57 7. Furjė serijos naudojimas siekiant išspręsti diferencialinių lygčių privačių išvestinių finansinių priemonių tyrime (gamtos reiškinys, gamybos proceso, valdymo sistemų ir kt.) Du veiksniai yra būtini: sukauptų žinių apie objektą lygis Matematinių aparatų kūrimo laipsnį. Šiuo metu buvo sukurta kita mokslinių tyrimų etape: fizinis matematinio modelio pavyzdys. Fizinė užduoties formuluotė (modelis) yra tokia: proceso kūrimo sąlygos ir pagrindiniai veiksniai, turintys įtakos jis yra aptinkamas. Matematinė formuluotė (modelis) yra apibūdinti fizinės kompozicijos pasirinktus veiksnius lygčių sistemos (algebrinio, diferencialo, integruoto ir tt) veiksniai. Užduotis yra teisingai nustatyta, jei tam tikroje funkcinėje erdvėje egzistuoja problemos sprendimas, vienintelis ir tęstinis priklauso nuo pradinių ir ribinių sąlygų. Matematinis modelis nėra identiškas nagrinėjamam objektui, tačiau jo apytikslis aprašymas iš laisvo mažų skersinių virpesių virpesių rezultatų bus laikomas vadovėliu. Leiskite styginių galai yra fiksuoti, o pati eilutė yra įtempta. Jei svertumėte eilutę nuo pusiausvyros padėties (pvz., Norėdami vėluoti arba paspausti jį), eilutė prasidės 57

58 svyruoja. Mes manome, kad visi eilutės taškai juda statmenai savo pusiausvyros pozicijai (skersinių virpesių), ir kiekvieną kartą eilutė yra toje pačioje plokštumoje. Paimkite į šią plokštumą XOU stačiakampio koordinačių sistemą. Tada, jei pradiniame laiko momentu t \u003d eilutė buvo išdėstyta išilgai uolų ašies, tada u reikštų eilutės nukreipimą nuo pusiausvyros padėties, tai yra, eilutės taško padėtis su abscisa x vieta savavališkas momentas t atitinka funkciją u (x, t). Su kiekviena fiksuota t, grafiko funkcija u (x, t) reiškia svyruojančių eilutės formą laiku t (32 pav.). Su pastovia vertė x, funkcija u (x, t) suteikia taško judesio įstatymą su Abscessa x palei tiesia, lygiagrečiai OU ašies, už šio judėjimo greitį, ir antrąjį darinį 2 darinį U t 2 pagreitis. Fig. 32. pajėgos, taikomos neabejotinai mažam styginių ruožui, bus lygtis, su kuria turi būti patenkinta funkcija u (x, t). Norėdami tai padaryti, mes padarysime daugiau supaprastinti prielaidas. Mes apsvarstysime absoliučiai galią - 58

59 Koy, tai yra, mes manome, kad eilutė neperpina lenkimo; Tai reiškia, kad eilutėje atsirandantys įtempiai visada skirti jo momentinio profilio liestiniam liestiniam. Manoma, kad eilutė yra elastinga ir nutukusi gerklės teisė; Tai reiškia, kad įtempimo jėgos dydžio pokytis yra proporcingas eilutės ilgio pokyčiui. Mes manome, kad eilutė yra vienoda; Tai reiškia, kad jo linijinis tankis ρ yra pastovus. Mes nepaisome išorinių jėgų. Tai reiškia, kad mes laikome nemokamus virpesius. Mes mokėsime tik mažus styginius svyravimus. Jei nurodysite φ (x, T) tarp abscisos ašies ir liestinės prie abscisės taško x tuo metu t, osciliacijų būklė yra dėl φ (x, t) vertės gali būti nepaisoma, palyginti su φ (x, t), t.e. φ 2. Kadangi kampas φ yra mažas, tada cosφ 1, φ φ u yra todėl vertė (uxx,) 2 taip pat galima apleisti. Iš čia ji nedelsdama taip, kad virpesių procese galime pamiršti bet kokios eilutės ilgio pokyčius. Iš tiesų, eilutės ilgis m 1 m 2, kuris yra suprojektuotas į abscissa ašies atotrūkį, kur x 2 \u003d x 1 + x yra lygi l \u003d x 2 x () 2 u dx x. X Mes parodome, kad su mūsų prielaidomis įtempimo jėga t bus pastovi visoje eilutėje. Paimkite šią eilutės skyrių M 1 m 2 (32 pav.) Laiku t ir pakeisti išmestos dalies veikimą - 59

60 vienetų įtempimo jėgos t 1 ir t 2. Kadangi pagalba visos styginių taškai juda lygiagrečiai ou ašių ir išorinių jėgų trūksta, iš įtempimo jėgų išorės ašies suma turėtų būti nulis: T 1 cosφ (x 1, t) + t 2 cosφ (x 2, t) \u003d. Nuo čia dėl kampų mažėjimo φ \u003d φ (x 1, t) ir φ 2 \u003d φ (x 2, t), mes darome išvadą, kad t 1 \u003d t 2. žymi bendrą t 1 \u003d t vertę 2 per T. dabar apskaičiuojame f u iš tų pačių jėgų sumą OU ašyje: F u \u003d t sin ę (x 2, t) t sin φ (x 1, t). (2) Kadangi mažų kampų nuodėmės φ (x, t) tg φ (x, t) ir tg φ (x, t) u (x, t) / x, tada lygtis (2) gali būti perrašyta taip f u t (TG φ (x 2, t) tg φ (x 1, t)) (u TX (x 2, t) u) x (x 1, t) xx t 2 UX 2 (x 1, t) x. Kadangi X1 punktas yra pasirinktas savavališkai, tada f u t 2 u x2 (x, t) x. Po visų jėgų, veikiančių M 1 m 2 skyriuje, mes taikysime jam antrą Niutono įstatymą, pagal kurį masės produktas pagreitinti yra lygus visų dabartinių jėgų sumai. Styginių M 1 m 2 masė yra m \u003d ρ l ρ x, o pagreitis yra 2 u (x, t). "Newton" lygtis t 2 yra forma: 2 u t (x, t) x \u003d u 2 α2 2 x2 (x, t) x, kur α 2 \u003d t ρ yra pastovus teigiamas skaičius. 6.

61 pjovimas į x, mes gauname 2 u t (x, t) \u003d u 2 α2 2 x2 (x, t). (21) Todėl mes gavome linijinę homogeninę diferencialinę lygtį su antrosios eilės privačiomis išvestinėmis priemonėmis su pastoviais koeficientais. Jis vadinamas styginių osciliacijų lygtimi arba vienatais bangos lygtis. (21) lygtis iš esmės performuluoja Newtono įstatymą ir apibūdina styginių judėjimą. Tačiau fizinės užduoties formuluotės reikalavimai buvo nustatyti, kad styginių pabaiga yra fiksuota ir tam tikru metu yra eilutės padėtis. Šios sąlygos bus registruojamos šiomis sąlygomis: a) Mes manome, kad styginių galai yra pritvirtinti taškuose x \u003d ir x \u003d l, ty mes manome, kad visiems t, santykiai u (t) \u003d, u ( l, t) \u003d; (22) b) Mes manome, kad tuo metu t \u003d eilutės padėtis sutampa su grafiko funkcija F (x), t.y., mes manome, kad lygybė u (x,) \u003d f (x,) \u003d f ( x); (23) b) mes manome, kad tuo metu t \u003d taškas su abscisa x yra suteikta greitis g (x), t.e. Mes manome, kad u (x,) \u003d g (x). (24) t santykis (22) vadinamos ribinėmis sąlygomis, o santykiai (23) ir (24) vadinami pradinėmis sąlygomis. Matematinis mažo skersinio 61 matematinis modelis 61

62 Stygos svyravimai yra išspręsti lygtį (21) su ribinėmis sąlygomis (22) ir pradinėmis sąlygomis (23) ir (24), iš laisvų mažų skersinių virpesių eilutės lygties sprendimas pagal Fourier metodą išspręsti lygtį (21) lygtis X l,< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. Pakeičiant (25) (21), mes gauname: x t \u003d α 2 x t, (26) arba t (t) α 2 t (t) \u003d x (x) x (x). (27) Jie sako, kad įvyko kintamieji atskyrimas. Nuo X ir T nepriklauso vienas nuo kito, kairėje pusėje (27) nepriklauso nuo x, o iš t ir bendra šių santykių vertė 62

63 turėtų būti nuolatinis, kuris yra pažymėtas λ: t (t) α 2 t (t) \u003d x (x) x (x) \u003d λ. Iš čia mes gauname du paprastus diferencialinės lygtys: X (x) λx (x) \u003d, (28) t (t) α 2 λt (t) \u003d. (29) Šiuo atveju ribinės sąlygos (22) imsis formą x () t (t) \u003d ir x (l) t (t) \u003d. Kadangi jie turi būti atliekami visiems t, t\u003e, tada x () \u003d x (l) \u003d. (3) Rasime lygties (28) lygties sprendimus, atitinkančius ribines sąlygas (3). Apsvarstykite tris atvejus. 1 atvejis: λ\u003e. Nurodo λ \u003d β 2. lygtis (28) yra x (x) β2 x (x) \u003d. Jos būdinga lygtis K 2 β2 \u003d turi šaknis k \u003d ± β. Taigi, bendras sprendimas Lygtys (28) turi X formą (x) \u003d c e βx + de βx. Turime pasirinkti konstantą C ir D, kad būtų laikomasi ribinių sąlygų (3), t.e. x () \u003d c + d \u003d, x (l) \u003d c e βl + de βl \u003d. Nuo β, ši lygčių sistema turi vieną tirpalą c \u003d d \u003d. Todėl X (x) ir 63

64 u (x, t). Taigi, 1 atveju, gavome trivialus sprendimą, kurį mes to nepadarysime. 2 atvejis: λ \u003d. Tada lygtis (28) yra x (x) \u003d ir jo tirpalas akivaizdžiai apibrėžiamas pagal formulę: X (x) \u003d C x + d. Pakeitus šį tirpalą ribinėmis sąlygomis (3), mes gauname x () \u003d d \u003d ir x (l) \u003d cl \u003d cl \u003d, tai reiškia c \u003d d \u003d. Todėl X (x) ir u (x, t) ir vėl gavome trivialų sprendimą. 3 atvejis: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 Ateityje mes suteiksime tik teigiamas n \u003d 1, 2 vertes, ... nuo neigiamo N, tos (rūšių nπ) n \u003d yra vadinami savo numeriais, ir Funkcijos xn (x) \u003d C n sin πnx su savo diferencialinės lygties (28) funkcijomis su ribinėmis sąlygomis (3). Dabar išspręsime lygtį (29). Jai būdinga lygtis turi formą k 2 α 2 λ \u003d. (32) L 2 Kadangi mes sužinojome, kad ne trivialūs tirpalai x (x) lygties (28) yra prieinami tik neigiamam λ, lygus λ \u003d N2 π 2, tada mes apsvarstysime tokį λ. (32) šaknys (32) yra k \u003d ± Iα λ, ir lygčių sprendimai (29) turi formą: t n (t) \u003d N sin πnαt + b n cos πnαt, (33) l l l kur n ir b n savavališkai pastovi. Pakeičiant formules (31) ir (33) (25) (25), mes rasime privačius lygties (21) sprendimus, kurie atitinka krašto sąlygas (22): (JT (x, t) \u003d bn cos πnαt + sin πnαt) cn Nuodėmė πnx. Pristatykite daugiklį C n į laikiklį ir įvedant paskyrimą C N a n \u003d bn ir b n c n \u003d an, parašykite un (x, t) formoje (JT (x, t) \u003d cos πnαt + bn sin πnαt) nuodėmės πnx . (34) L L L 65

66 styginių svyravimai, atitinkantys tirpalus, u n (x, t) yra vadinami savo styginių svyravimais. Kadangi lygtis (21) ir ribinės sąlygos (22) yra linijinės ir homogeninės, tada linijinis derinys tirpalų (34) (u (x, t) \u003d a cos παt + bn sin πnαt) nuodėmės πnx (35) lll bus išspręsta Pagal (21) lygtį atitinkančiomis ribines sąlygas (22) su specialiu pasirinkimu koeficientų AN ir BN, kuris užtikrina vienodą konvergenciją eilės. Dabar mes dabar pasirinksime koeficientus ir BN sprendimus (35), kad jis atitiktų ne tik ribą, bet ir pradines sąlygas (23) ir (24), kur f (x), g (x) nurodytos funkcijos (ir F ( ) \u003d f (l) \u003d g () \u003d g (l) \u003d). Manome, kad F (x) ir g (x) funkcijos atitinka keturių serijos skilimo sąlygas. Pakeičiant (35) t \u003d, mes gauname u (x,) \u003d a n nuodėmė πnx l \u003d f (x). Serija (35) pagal T ir pakeičiant T \u003d, mes gauname UT (x,) \u003d πnα bn sin πnx l \u003d g (x), ir tai yra funkcijų f (x) ir g (x) skilimas "Fourier" serija. Todėl, n \u003d 2 l l f (x) nuodėmės πnx l dx, b n \u003d 2 l g (x) nuodėmės πnx dx. πnα l (36) 66

67 pakeičiant tyrimą N ir B N iš eilės (35), mes gauname lygtį (21), atitinkančią ribines sąlygas (22) ir pradines sąlygas (23) ir (24). Taigi, mes išsprendėme nemokamų mažų skersinių virpesių problemą. Išsiaiškinkite fizinę reikšmę EigenFunctions u n (x, t) laisvo svyravimų, apibrėžtų pagal formulę (34). Mes perrašome jį į formą, kur u n (x, t) \u003d α n cos πnα l α n \u003d a 2 n + b2 n, (t + Δ n) nuodėmės πNX, (37) l πNα Δ n \u003d arctg b n. L a formulė (37) rodo, kad visi eilutės taškai daro harmonines virpesius su tuo pačiu dažniu ω n \u003d πNα ir πNα Δ N fazė. Oscilacijos amplitudė priklauso nuo Abscessa x iš eilutės taško ir yra lygus α n n nuodėmės πnx. Su tokiu svyravimu, visi eilutės taškai vienu metu pasiekia maksimalų nuokrypį vienoje ar kitoje pusėje, ir tuo pačiu metu perduoti pusiausvyros padėtį. Tokie virpesiai vadinami stovinčiomis bangomis. Nuolatinė banga turės N + 1 vis dar apibrėžtą nuodėmės πnx lygties šaknų taške \u003d intervale [, l]. Fiksuoti taškai vadinami nuolatiniais bangų mazgais. Viduryje tarp mazgų, yra taškų, kuriuose nuokrypiai pasiekia maksimalų; Tokie punktai vadinami pūkais. Kiekviena eilutė gali turėti savo virpesius griežtai apibrėžtus dažnius ω n \u003d πnα, n \u003d 1, 2, .... Šie dažniai vadinami savo eilutės dažniais. Mažiausias l tonas, kuris gali gaminti stygas yra nustatomas 67

68 Žemo dažnio ω \u003d π t ir vadinama pagrindiniu eilutės tonu. Likę tonai, atitinkantys L ρ dažnių ω N, N \u003d 2, 3, ... vadinami obramstones ar harmonika. Siekiant aiškumo, mes parodysime tipiškus styginių profilius, skleidžiančius pagrindinį toną (33 pav.), Pirmasis Obertonas (34 pav.) Ir antrasis Obertonas (35 pav.). Fig. 33. Styginių profiliai, skelbti pagrindinį toną. 34. Styginių profilio skelbimas pirmųjų operton ryžių. 35. Stygos profilis, kurį paskelbė antrasis Obtonas Jei eilutė atlieka nemokamus virpesius, nustatytus pagal pradines sąlygas, atrodo, kad funkcija u (x, t), atrodo, matyti iš formulės (35), kaip atskirų harmonikų suma. Taigi, savavališkas svyravimas 68

69 stygos yra stovinčių bangų superpozicija. Tuo pačiu metu, eilutės pobūdis (tonas, garso galia, Timbre) priklausys nuo individualios harmonikų jėgos amplitudų, aukščio ir už sumišimo eilutės garso balso sužadina svyravimus oras, suvokiamas žmogaus ausies kaip garso, paskelbto eilutėje. Garso galia būdinga virpesių energija ar amplitudė: didesnė energija, tuo didesnė garso galia. Garso aukštis nustatomas pagal jo dažnį arba virpesių laikotarpį: kuo didesnis dažnis, tuo didesnis garsas. Garso timbre yra nustatomas pagal Objektų buvimas, energijos platinimas pagal harmonikų, t.e., sužadinimo metodą virpesių metodas. Obpones amplitudes, apskritai, mažiau amplitudės pagrindinio tono, ir operton fazė gali būti savavališka. Mūsų ausis nėra jautrus virpesių fazei. Palyginkite, pavyzdžiui, dvi kreivės Fig. 36 pasiskolino. Tai yra garso įrašymas su tuo pačiu pagrindiniu tonu, išgautas iš klarneto (a) ir fortepijono (B). Abu garsai nėra paprasti sinusoidiniai virpesiai. Pagrindinis garso dažnis abiem atvejais yra tas pats ir sukuria tą patį toną. Tačiau kreivių brėžiniai yra skirtingi, nes pagrindiniam tonui taikomas skirtingi obhrothon. Tam tikra prasme šie brėžiniai rodo, kas yra Timbre. 69.

Hiperbolinės tipo lygtys. Begalinės ir pusiau begalinės eilutės virpesiai. Furjė metodas Fourier metodas Nuolatinės bangos 4 paskaita 4.1 hiperbolinės tipo lygtys. Begalinio ir pusiau begalinio virpesiai

Maskvos valstybinis civilinės aviacijos universitetas V.M. Lyubimov, E.A. Zhukova, V.A. Wokova, yu.a. "Shuririnov Ma T e m a ir k a r i" skelbia disciplinų tyrimą ir terminus

Rusijos Švietimo ir mokslo ministerija Federalinė Valstybinė aukštojo profesinio mokymo švietimo įstaiga MATI Rusijos valstybinis technologinis universitetas, pavadintas K. E. Tsiolkovsky

Baltarusijos Respublikos švietimo ministerija UO "Vitebsko valstybinis technologijos universitetas" tema. Teorinės ir taikomosios matematikos katedros "eilutės". Sukurta DC. E.B. DUNIN. Priežiūra

Federalinė švietimo agentūra Federalinė valstybinė švietimo įstaiga aukštojo profesinio mokymo Pietų Federalinis universitetas R. M. Gavrilova, G. S. Kostotskaya metodiškas

"Furjier" serijos "Fourier" serijos furlier serijos furlier serijos okupacija "Fourierewise" funkcijų vietos sistemoms "FoureweLe" nuolatinės funkcijos bendrosios "Fourier" serijos 3 nelygybė Bessel ir Furjė serijos konvergencija

Serijų teorija Serijos teorija yra esminė matematinės analizės dalis ir nustatoma teorinė ir daugybė praktinių programų. Yra skaitmeninių ir funkcinių skaičių.

Furjė serijos turinys 4 periodinės funkcijos koncepcija 4 trigonometrinis polinominis 6 3 Funkcijų stačiakampių funkcijos 4 trigonometriniai Furjė serija 3 5 Furjė eilutė net ir nelyginėms funkcijoms 6 6 Skilimas

Federalinė Švietimo agentūra Maskvos valstybinio geodezijos universitetas ir kartografija (Miigaik) metodinės instrukcijos ir užduotys nepriklausomam darbui aukštesnės matematikos skaitmeniniam skaičiui

Paskaita 4. Harmoninė analizė. Furjė serijos periodinės funkcijos. "Harmonic" analizė mokslo ir technologijų dažnai turi susidoroti su periodiniais reiškiniais, t. Y., tie, kurie kartojami per

"Temic V" serijai "Fourier" paskaita 6 periodinės funkcijos skaidymas "Fourier" eilėje Daugelis gamtos ir technologijų procesų turi savybių pakartoti po tam tikrų intervalų tokių procesų

Metodinės gairės atsiskaitymų užduočių tuo didesnių matematikos norma "įprastos diferencialinės lygtys serijos dvigubų integralų" dalis ш tema rangų lentelės Skaitinių eilučių konvergencijos ir skirtumų eilučių eilutės

6 Fourier eilutės 6 Ortogoninės funkcijos Furjė funkcijų dėl funkcijų funkcijų φ () ir ψ () apibrėžta ir integruota į segmentą [], yra vadinami stačiakampiu šiame segmente, jei

Tam tikras neatsiejamas. Neatsiejama sumas ir tam tikras neatsiejamas leiskite funkcijai y \u003d f (), apibrėžta segmente [, B], kur yra, kur< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

5 Maitinimo eilutės 5 Galios eilutės: apibrėžimas, regiono regiono funkcinė eilutė (A + a) + k + a () + k a) ((5) kur, a, a, k, a, k kai kurie numeriai yra vadinami galingu numeriu

Baltarusijos valstybinio universiteto Taikomosios matematikos ir informatikos fakultetas Aukštojo matematikos katedra Švietimo ir metodinis vadovas Taikomosios matematikos ir informatikos fakulteto studentams

Apsvarstykite keletą pavyzdžių. Pavyzdys. Mes surasime begalinės geometrinės progresavimo apie šio serijos AQ + ... + AQ N + ... (A). n \u003d aq n. Apskaičiuokite jo dalines sumas. Jei q \u003d, tada

1.1 užduotis. Rasti konkrečiame regione skiriasi nuo identiškų nulinių sprendimų y \u003d y (x) diferencinės lygties, kuri atitinka nustatytas ribines sąlygas (Sturm Liuville užduoties) Sprendimas: Apsvarstykite

Matematinė analizė Tema: tam tikras nesuprantamas Integruotas dėstytojas Pakhomova E.G. 2017 II skyrius. Tam tikras neatsiejamas ir jo taikymas 1. Specifinis neatsiejamas ir jo savybės 1. Užduotys,

Paskaita 8 4 Užduotis Sturm Lioville Apsvarstykite pradinę ribinę problemą diferencinės lygties antrosios eilės dalinių darinių, apibūdinančių mažų skersinių styginių eilutės svyravimų, yra laikoma

Teksto paaiškinimas: Ženklas yra skaitomas kaip "ekvivalentu" ir rodo, kad lygtys ant ženklo dešinėje ir kairėje nuo žymens nustato sprendimų rinkinį sutampa, IR ženklas rodo tikrus numerius, prisijunkite

82 4. Funkcinės ir galios eilutės 4.2. 3 pamoka 4.2. 3 pamoka 4.2. Taylor serijos serijos skaidymas apibrėžimas 4.2. Tarkime, kad funkcija y \u003d f (x) yra be galo diferencijuojama kai kuriose aplinkoje

Rusijos švietimo ir mokslo ministerija Federalinė valstybinė biudžeto švietimo įstaiga aukštojo profesinio mokymo "Samaros valstybinis techninis universitetas" K A F E D R taikoma matematika

Federalinė geležinkelių transporto agentūra Uralo valstybinis ryšių universitetas departamento departamentas "Aukštesnės ir taikomos matematikos" N. P. Chuev harmoniniai analizės elementai metodiškai

Paskaita 3 Taylor's Rangs ir Maclorena galios taikymas eilėmis funkcijų skilimas į galios eilių Taylor ir Maclorena už programų serija Svarbu suprasti šią funkciją galios eilėje, tos funkcijos

C Lavrenchenko wwwwrckoru paskaita "Fourier Transformation" integruotos transformacijos metodo sąvoka yra vienintelis matematinės fizikos metodas yra galingas sprendimas

Funkcijos (Riemann) integracija ir konkretūs neatskiriami problemų sprendimo pavyzdžiai 1. Nuolatinė funkcija F (x) \u003d C yra integruojama, nes bet kokiam skaidiniui ir bet kokiam taškų pasirinkimui ξ Aš integruojant

Aš vertinu, užduotis. Įrodyti, kad RIEMANN funkcija, jei 0, M M R (), jei, M, M 0, ir frakcija yra sutrikimas, 0, jei neracionaliai, pertrauka kiekviename racionaliame taške ir yra nepertraukiamai kiekvienoje neracionalioje vietoje. Sprendimas.

1 2 Turinys 1 Fourier eilutės 5 1.1 trigonometriniai Furjė serija ............ 5 1.2 Tik sin & cos ................... .. 7 1.3 Furjė serija sudėtingoje formoje ........... 11 1,4 f (x) \u003d ck? .................... .....

Matematinės fizikos lygtys 1. Diferencialinės lygtys su privačių darinių lygtis, jungianti nežinomą funkciją U (x 1, x 2, ..., x n), nepriklausomi kintamieji x 1, x 2, ..., x n ir privatūs

Paskaita 4. Bangų lygtis 1. Virtuvės virpesių lygtis 2. Strypo išilginių svyravimų lygtis 3. Pradinės sąlygos, ribinės sąlygos 4. Užduočių nustatymas 1. Styginių virpesių lygties produkcija.

1. Elektrostatikai 1 1. Elektrostatikos pamoka 6 kintamųjų atskyrimas Carteso koordinatėse 1.1. (1.49 užduotis) Z \u003d plokštuma įkrauta tankiu σ (x, y) \u003d σ sin (αx) nuodėmė (y), kur σ, α, β yra pastovi.

Modulio temos funkcinės sekos ir vienodo sekų konvergencijos ir serijos galios eilių paskaitų funkcinių sekų ir eilučių apibrėžimas tolygiai

Parabolinės rūšies lygtys. Kintamųjų atskyrimo metodas Homogeninė ribinė vertė Problema Šaltinio funkcija Heterogeninė terminio laidumo lygtis 7 Paskaita 7.1 lygčių parabolinės rūšies lygtys. Atskyrimo metodas

Paskaita Skaitmeniniai eilutės Konvergencijos skaitmeninių serijos ženklų konvergencijos begalinės ekspresijos ženklai + + + + + + + sudaryto iš begalinio, vadinamo skaitmeninio numerio narių,

35 7 trigonometriniai Furjė serija Fourier eilučių periodinėms funkcijoms su T. tegul f (x) būti gabalas - nuolatinis periodinė funkcija su laikotarpiu T. Apsvarstykite pagrindinę trigonometrinę sistemą

Metalurgijos fakultetas Aukštojo matematikos Elews Metodical Instrukcijos Novokuznetsk 5 Federalinė agentūra švietimo valstybinės švietimo įstaigos aukštojo profesinio mokymo

Matematikos katedra ir informatikos elementų aukštojo matematikos švietimo ir metodinio komplekso studentams CPA, studentai, naudojant nuotolinio technologijų modulio diferencialo skaičiavimo kompiliatorius:

9. pred-panašios ir neribotos integruotos 9 .. Tarkime intervale I r nustatyta funkcija F (). Funkcija f () yra vadinama primityvi funkcija f () intervalu I, jei f () \u003d f () bet aš ir primityviai

Vienos kintamojo darinio sąvokos funkcijų diferencijavimas, jo geometrinis ir fizinės problemos reikšmės, dėl kurio susidaro tangencinės s nustatymo sąvoka su Y F (X) nustatymo sąvoka X punkte A taške; f (

Hiperbolinės tipo lygtys. Begalinės ir pusiau begalinės eilutės virpesiai. DALUBER BEINITE eilutės metodas. DALambel formulės pusiau begalinė eilutė 3 paskaita 3.1 hiperbolinių tipo lygtis.

Turinys Įvadas. Pagrindinės sąvokos .... 4 1. Integruotos lygtys Volterry ... 5 galimybės namų darbams .... 8 2. Volterra integralo lygtis. 10 namų darbų galimybių .... 11

Eilutės. Skaitmeninės eilutės. Pagrindiniai apibrėžimai suteikiama begalinė numerių išraiška (begalinė suma) a, a 2, ..., n, ... a i \u003d a + a 2 + + a n + ... () i \u003d vadinama skaitmenine. Skaičiai. \\ T

8. Maitinimo eilutės 8 .. Funkcinės serijos C N (Z) N, (8.) N \u003d kai C n skaitmeninė seka, R fiksuotas numeris, ir Z R yra vadinami galia kartu su C N koeficientais. Pakeičiant kintamuosius

~ ~ Nereikia ir specifinė integruota primityvios ir neribotos integralo samprata. Apibrėžimas: F funkcija yra vadinama Primityvi, atsižvelgiant į F funkciją, jei šios funkcijos yra susijusios su toliau

3724 eilių daugelio ir kreivių integralai 1 darbo programa sekcijų "eilių daugiklių ir kreivių integralų" 11 skaitmeninių eilučių skaitinės serijos skaitmeninių eilučių koncepcija būtinas konvergencijos ženklas

Valgykite. ORE matematinė analizė. Skaitmeninis ir funkcinės serijos NOVOSIBIRSK 200 2 MINO Apsaugos nuo Rusijos Gou VPO "Novosibirsko valstijos pedagoginis universitetas" E.M. ORE matematinė analizė.

Paskaita N 7. Galingas serija ir Taylor serija. Tada eilutės ..... Taylor .... 4. kai kurių elementarių funkcijų taikymas taylor ir macloren .... 5 4. Taikant galios eilutes .... 7. SSED

Kvadratinės lygtys Turinys Kvadratinės lygtys ... 4. ir kvadratinių lygčių tyrimas ... 4 .. kvadratinių lygtis su skaitmeniniais koeficientais ... 4 .. Išspręskite ir ištirkite kvadratinių lygčių santykį

Užduočių skyrius su parametrų komentarais Užduotys su parametrais yra tradiciškai sudėtingi naudojimo struktūros užduotys, reikalaujantys iš pareiškėjo ne tik visų metodų nuosavybės ir įvairių sprendimų priėmimo

Diferencinis skaičiavimas Įvadas į matematinę analizę sekos ir funkcijos riba. Neapibrėžtumo atskleidimas. Gauta funkcija. Diferenciacijos taisyklės. Programos darinys

Furjė serija Ortogoninės sistemos funkcijų nuo Atsižvelgiant į algebra lygybę taško, kai - šios klasės funkcijos - koeficientai nuo R arba C tiesiog reiškia, kad vektorius yra linijinis derinys vektorių

1. Tam tikras neatsiejamas 1.1. Leiskite f būti ribota funkcija, nurodyta segmente [, b] R. segmento skaidymas [, b] yra vadinamas tokiu taškų rinkiniu τ \u003d (x, x 1, ..., xn 1, xn) [ , b], kuris \u003d x< x 1 < < x n 1

Chulflage A A A A A A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-A-AM yra vadinamas daugiau bendro rūšies serija: A A (a) (a) (a) (), kur

turėtų:

1) atkreipti tvarkaraštį f (x) dėl atotrūkio bent jau dviejų laikotarpių ilgis rodo, kad ši funkcija yra periodinė;

2) Nubraižykite tvarkaraštį S (x) Panašiai, kad būtų matoma, kokiais klausimais f (x) ¹s (x);

3) Apskaičiuokite "Fourier" koeficientus ir parašykite "Fourier" eilutę.

Užduotys

№1. Puikus

Sprendimas. pastebėti, kad f (x) Nustatykite ilgio ilgį T \u003d 4.. Nes. f (x) Manoma, kad jis yra periodinis, šis skaičius yra jo laikotarpis, tada - l \u003d 2.

1) grafikas f (x):

2) grafikas S (x):

Rodyklės linijų galuose rodo, kad funkcija nepriima verčių, nustatytų iš nurodytos intervalo išraiškos. Lyginant grafikus f (x) ir. \\ T S (x) Tai aiškiai matoma, kad pertraukos taškuose f (x) ¹s (x).

3) Apskaičiuokite "Fourier" koeficientus. Tai gali būti padaryta formulėmis (3 *):; ; . Tiksliai:; Taigi,

Skilimas f (x) "Fourier" turi formą:

Komentarai. 1) integruojant [-1;3] Šis segmentas buvo sugadintas ir. \\ T nes. Dėl šių segmentų f (x) Nustatykite skirtingas vertes.

2) Apskaičiuojant koeficientus naudojami integralai: ir, kur a \u003d Const..

№2 . Puikus

Sprendimas. Čia T \u003d 2., l \u003d 1..

"Fourier" serija turi formą: kur; ; nes. l \u003d 1..

1) grafikas f (x):

2) grafikas S (x):

№3. Suskaidyti "Fourier" sinose

Sprendimas. Atkreipkite dėmesį, kad Furjė sinusuose pradedami tik nelygios funkcijos. Nes. f (x) Apibrėžta tik. \\ T x\u003e 0, xî (0; 2) è (2; 3)tada tai reiškia, kad simetriškai intervalui (-3; -2) è (-2; 0) f (x)reikia tęsti, kad lygybė f (-x) \u003d -f (x). Todėl atotrūkio trukmė f (x) Jis nustatomas kaip nelyginė funkcija, lygi 6 T \u003d 6, l \u003d 3. "Fourier" serija. \\ T f (x) Jis turi formą :, kur, n \u003d 1, 2, 3, (pagal formules (5 ")).

1) grafikas f (x).

Norėdami atkreipti grafiką f (x) Kaip nelyginė funkcija, pirmiausia atkreipkite dėmesį į tvarkaraštį (0; 2) è (2; 3)Ir tada pasinaudokite tuo, kad nelygios funkcijos tvarkaraštis yra simetriškas koordinatės pradžioje. Iš šių aplinkybių mes gauname tvarkaraštį f (x) ant (-3; -2) è (-2; 0). Tada tęskite f (x) T \u003d 6..

2) grafikas S (x).

Tvarkaraštis. \\ T S (x) Skiriasi nuo tvarkaraščio f (x) pertraukos taškuose f (x). Pavyzdžiui, t. x \u003d 2 f (x)nenustatyta, ir S (x) turi x \u003d 2. Reikšmė, lygi pusiau pusiau pusiausvyrai f (x), tiksliai: kur.

Taigi, tada skilimas f (x) Furjė turi formą :.

№4 . Išsiųsti Fourier apie kosiną.

Sprendimas Šis sprendimas. Atkreipkite dėmesį, kad tik netgi funkcijos yra pradėtos iš eilės "Fourier Cosine". Nes. f (x) Nustatykite tik. \\ T x\u003e 0, xî (0; 2) è (2; 3], tada tai reiškia, kad simetriškai intervalui [-3; -2) è (-2; 0) f (x)būtina tęsti, kad būtų atlikta lygybė: f (-s) \u003d f (x). Todėl atotrūkio trukmė f (x) Nustatykite kaip netgi funkcija yra lygi 6, tada T \u003d 6, l \u003d 3. "Fourier" serija šioje byloje atrodo:

kur; ; n \u003d 1,2, ... (pagal formules (4)).

1) grafikas f (x).

Norėdami atkreipti grafiką f (x) Kaip net funkcijos, pirmiausia atkreipkite tvarkaraštį f (x) ant (0; 2) è (2; 3]Ir tada pasinaudokite tuo, kad netgi funkcijos grafikas yra simetriškas apie ordinato ašį. Iš šių aplinkybių mes gauname tvarkaraštį f (x) ant [-3; -2) è (-2; 0). Tada tęskite f (x) apie visą skaitmeninę tiesioginę kaip periodinę funkciją su laikotarpiu T \u003d 6..

Čia yra tvarkaraštis f (x) Parengta dviem pilnais funkcijų laikotarpiais.

2) grafikas S (x).

Tvarkaraštis. \\ T S (x) Skiriasi nuo tvarkaraščio f (x) pertraukos taškuose f (x). Pavyzdžiui, t. x \u003d 0 f (x)nenustatyta, ir S (x) turi reikšmę: , todėl tvarkaraštis S (x) Nepertraukiama t. x \u003d 0., Skirtingai nuo tvarkaraščio f (x).

Skilimas f (x) Iš eilės "Fourier" "Cosineses", ji turi formą :.

№5. Puikus f (x) \u003d | x |, xî (-2; 2)..

Sprendimas. Pagal sąlygą, f (x) yra netgi veikia (-2;2) ; tie. Jos Furjė serijoje yra tik kosmenims, o T \u003d 4, l \u003d 2, ,

kur; ; n \u003d 1, 2,

1) grafikas f (x):

2) grafikas S (x):

3), nes | X | \u003d X.dėl x\u003e 0.; .

Tada skilimas f (x) Furjė turi formą :. Atkreipkite dėmesį, kad integruojant išraiškas arba taikant integracijos formulę dalių: kur u \u003d x; Dv \u003d cos (kirvis) dxarba. \\ T DV \u003d SIN (AX) DX.

№6. Padalinkite Fourier serijos funkciją: a) intervale (-?); b) intervale (0, 2?); c) intervale (0,?) sinusų eilėje.

Sprendimas. a) Funkcijos grafikas su 2? - periodinis tęsinys yra

Funkcija tenkina Dirichlet teorem sąlygas, todėl jis gali būti suskaidytas į "Fourier" seriją.

Apskaičiuokite "Fourier" koeficientus. Kadangi funkcija yra net, tada bn \u003d 0 (n \u003d 0, 1, 2, ...) ir (n \u003d 0, 1, 2, ...).

Norint apskaičiuoti šį neatsiejamą, naudojama integracijos formulė konkrečioje integrale. Gauti

Furjė serija šios funkcijos turi formą. Dėl Dirichle ženklo ši serija reiškia funkciją x2 intervale (-?).

b) intervalas (0, 2?) nėra simetriškas koordinatės pradžioje ir jo ilgis 2 l. \u003d 2?. Apskaičiuokite Fourier koeficientus formulėmis:

Todėl Fourier turi formą. Pagal Digichlet teoremą serijos konverguojančios generuoti funkcijas X? (0,2?), Ir 0 ir 2 punktuose? prasmę. Iš eilės sumos suma turi formą

c) Funkcija suskaidoma į sinuso eilutę, turėtų būti keista. Todėl mes suteiksime nurodytą funkciją x2 (-π, π) nelyginis būdas, t.y. Mes manome, kad funkcija. Dėl šios funkcijos f (x) mes turime a \u003d 0 (n \u003d 0, 1, 2, ...) ir

Norimas skilimas turi formą.

Iš eilės sumos suma turi formą

Atkreipkite dėmesį, kad taškuose x \u003d (-π, π), Fourier eilutės konverguojančios iki nulio.

№7 Fourier grafiškai nurodyta funkcija:

Sprendimas Šis sprendimas . Mes gauname aiškią f (x) išraišką. Funkcijos grafikas yra tiesia linija, mes naudojame lygtį tiesiai į formą. Kaip matyti iš brėžinio ,, i.e. f (x) \u003d x - 1 (-1 -1< x < 1) и период Т = 2.

Ši funkcija atitinka DIRICELLET sąlygas, todėl jis suskaido į "Fourier" serijas. Apskaičiuokite "Fourier" koeficientus ( l. = 1):

; (n \u003d 1, 2, ...);

"Fourier" serija F (x) turi vaizdą

Jis reiškia funkciją f (x) ne -1< x < 1, а в точках х0 = -1 и х0 = 1 ряд сходится к -1.

№8. Išsiųsti funkciją trigonometrinėje eilėje "Fourier" ant segmento ir nurodykite funkciją, prie kurios susidarančios serijos konvernes.

Sprendimas.Nubraižykite funkcijos tvarkaraštį, tęsdami periodiškai su laikotarpiu arba visą ašį. Tęstinė funkcija turi laikotarpį.

Patikrinkite pakankamų "Furjier" serijos konvergencijos (Dini-Lipschitsa, Jordan, Dirichlet) sąlygas.

Funkcija "Pievewise Monotonna" segmente: jis padidėja ir toliau. Tuo tarpu funkcija turi pirmųjų spragų.

Sužinokite funkcijos paritetą ar keistumą: funkcija nėra nei lygi arba nelyginė.

a) Jei funkcija yra nurodyta

b) Jei funkcija yra nustatyta

Sukurkite eilutę Fourier funkcija :.

Nurodykite funkciją, kuriai ši serija susilieja, naudojant dabartinius konvergencijos požymius: pagal Dirichle ženklą, "Fourier" funkcijų serija susilieja su suma:

№9. Pašalinkite funkciją "Fourier" sinchuose ant sinų ir su šio skilimo pagalba rasti skaitinės serijos sumą.

Sprendimas.Tęsti funkciją yra net (nelyginis) kelias (- p.0) arba (- l.0), tada periodiškai su 2 laikotarpiu p. arba 2 l. Tęskite visą ašį funkciją.

Mes tęsiame funkciją keistai, ir tada periodiškai, su laikotarpiu, tęsis jį į visą ašį.

Nubraižykite periodinio tęstinumo grafiką. Gausime formos funkciją:

Patikrinkite pakankamų "Furjier" serijos konvergencijos požymių sąlygas (Dini-Lipica, Jordan, Dirichlet).

INFORMACIJA FUNKCIJOS INTERVENCE IN Intervale: jis yra lygus -1 ir 1. Tuo tarpu funkcija turi pirmųjų spragų.

Apskaičiuokite "Fourier" koeficientus:

Jo Furjė koeficientai apskaičiuoja formulėmis:

Padarykite eilutę "Fourier" funkcija. .

Nurodykite funkciją, prie kurios ši serija bus susilieja, naudojant detektyvinius konvergencijos požymius.

Pagal Dirichle ženklą, kai kurių "Fourier" funkcija susilieja su sumos:

Todėl. \\ T

Vertybių pakeitimas, nurodykite nurodytos skaitmeninės serijos sumą.

Tikėjimas gaunančiu skilimą, mes rasime

kur, nes.

№10. Parašykite "Parcatoris" lygybę funkcijai ir, remiantis šia lygybe, suraskite skaitinės serijos sumą.

Sprendimas.Įdiekite, ar ši funkcija yra funkcija su integruojančia aikštė.

Funkcija yra tęstinė, todėl integruota į. Dėl tos pačios priežasties, jo aikštė integruota.

Apskaičiuokite Fourier koeficientus formulėmis:

Nuo nelygios funkcijos, tada jo keturrieji koeficientai apskaičiuoja formulėmis:

Apskaičiuokite integruotą.

Parašykite Formulės parseval:

Taigi formulės parseval turi formą

Surengta, jei reikia, aritmetiniai veiksmai dešinėje ir kairėje dalyje, norint gauti šios skaitmeninės serijos sumą.

Dalijimasis abiem lygybės dalimis, gauta 144, mes randame :.

№11. Rasti "Fourier" integruotas funkcijas

ir sukurti IT tvarkaraštį.

Sprendimas.Sukurti funkcijos grafiką.

Patikrinkite pakankamo "Fourier Integral" (Dini, Dirichlet-Jordano ar jų pasekmių konvergencijos sąlygų įvykdymą.

Funkcija yra visiškai integruota į atotrūkį, tęstinį, kai ir ir tuo metu yra pirmojo tipo atotrūkis. Be to, su funkcija turi ribotą darinį, o galutiniai ir kairieji dariniai yra nuliui. Sužinokite funkcijos paritetą ar keistumą. Funkcija nėra nei net ir keista. ; .

Taigi, arba,

Netoli Fourier Funkcijos f (x) intervalo (-π; π) yra vadinami trigonometriniu formos serija:
kur

Netoli Fourier funkcija F (x) intervalo (-l; l) vadinama trigonometriniu formos serija:
kur

Tikslas. Prisijungę skaičiuoklė Skirta suskaidyti funkciją F (x) iš eilės iš eilės.

Modulio funkcijoms (pvz., | X |) cosine skilimas.

Funkcijų įvedimo taisyklės:

Modulio funkcijoms naudokite cosine skilimą. Pavyzdžiui, už | X | Būtina įvesti funkciją be modulio, t.y. x.

"Fourier" serijos "Skirtingos" nepertraukiamos, dalijasi monotoniška ir ribota intervale (- l.;l.) Konverguojančios visą skaitmeninę ašį.

Furjė serijos S (x) suma:

• tai periodinė funkcija su 2 laikotarpiu l.. Funkcija u (x) yra vadinama periodiniais su laikotarpiu (arba T-Periodic), jei visiems x regionas R, U (x + t) \u003d u (x).
• intervale (- l.;l.) sutampa su funkcija f.(x.), išskyrus nutraukimo taškus
• pertraukos taškuose (pirma, nes funkcija yra ribota) f.(x.) Ir intervalo galuose yra vidurkiai:

.
Sakoma, kad funkcija išdėstyta "Fourier" serijoje intervale (- l.;l.): .

Jeigu f.(x.) - netgi funkcija, tada tik netgi funkcijos yra įtrauktos į jo skilimą, tai yra, b N.=0.
Jeigu f.(x.) - nelyginė funkcija, tada jo skilimas dalyvauja tik nelygios funkcijos, ty, n.=0

Netoli Fourier Funkcijos. \\ T f.(x.) intervale (0; l.) "Cosine Dougses" Skambinama eilutė:
kur
.
Netoli Fourier Funkcijos. \\ T f.(x.) intervale (0; l.) dėl daugelio lanko sinais Skambinama eilutė:
kur .
"Furjier" serijos suma pagal daugelio lankų kosiną yra net periodinė funkcija su 2 laikotarpiu l.Sutampa S. f.(x.) intervale (0; l.) Tęstinumo taškuose.
Iš "Furjier" serijos daugelio lankų sinarų suma yra nelyginė periodinė funkcija su 2 laikotarpiu l.Sutampa S. f.(x.) intervale (0; l.) Tęstinumo taškuose.
"Fourier" serija šioje intervale yra unikalumo nuosavybė, ty jei skilimas yra gaunamas bet kuriuo kitu būdu nei formulės naudojimas, pavyzdžiui, naudojant koeficientų pasirinkimą, šie koeficientai sutampa su formulėmis, apskaičiuotomis formulės.

1 pavyzdys. Uždėkite funkciją f (x) \u003d 1:
a) visu Fourier diapazone intervale(-π ;π);
b) iš eilės ant įvairių lankų sinarų intervale(0;π); sukurkite gautų "Furjier" serijos grafiką
Sprendimas Šis sprendimas:
a) skilimas į Furjė serijos intervalo (-π; π) turi formą:
,
ir visi koeficientai b N.\u003d 0, nes Ši funkcija yra net; šiuo būdu,

Akivaizdu, kad lygybė bus vykdoma, jei vartojate
bet 0 =2, bet 1 =bet 2 =bet 3 =…=0
Atsižvelgiant į unikalumo savybes, tai yra norimi koeficientai. Taigi norimas skilimas: arba tik 1 \u003d 1.
Šiuo atveju, kai serija vienodai sutampa su savo funkcija, iš Furjė serija sutampa su funkcijos grafiką visoje skaitmeninėje linijoje.
b) Skilimas intervalo (0; π) dėl daugialypių lankų turi formą:
Neįmanoma pasirinkti koeficientų, kad lygybė būtų vienodai neįmanoma. Mes naudojame koeficientų skaičiavimo formulę:


Taigi, netgi n. (n.=2k.) b N.\u003d 0, nelyginiam ( n.=2k.-1) -
Pagaliau, .
Mes sukuriame gautų "Furtier" serijos grafiką naudodami savo savybes (žr. Aukščiau).
Visų pirma, mes statome šios funkcijos grafiką tam tikru intervalu. Be to, naudojant numerio sumos tikslumą, mes tęsiame grafiką simetriškai koordinates pradžia:

Mes tęsiame periodiškai apie visą skaitmeninę ašį:


Ir pagaliau, atotrūkio taškuose užpildykite vertės vidurkį (tarp dešinės ir kairiosios ribos):

2 pavyzdys. Atmesti funkciją Intervale (0; 6) dėl kelių lankų sinais.
Sprendimas Šis sprendimas: Pageidaujamas skilimas turi formą:

Nuo kairiojo ir dešinės dalies lygybės yra tik funkcijos. Iš įvairių argumentų patikrinkite, ar jie atitinka bet kokias N (natūralaus!) Vertybes sinusų argumentus kairėje ir dešinėje dalims lygybės:
Arba, iš kur n \u003d 18. Tai reiškia, kad toks terminas yra dešinėje pusėje, o koeficientas su juo turi sutapti su koeficientu kairėje pusėje: b. 18 =1;
Arba, iš kur n \u003d 4. Tai reiškia b. 4 =-5.
Taigi, su koeficientų pasirinkimu, buvo galima gauti norimą skilimą.