Pronalaženje koeficijenata Fourierove serije. Određivanje koeficijenata broja od strane Fourierovih formula

Fourierov niz periodičnih funkcija sa periodom od 2π.

Fourierove serije omogućava vam da studirate periodične funkcije, razgrađujete ih u komponente. Varijable i naponi, pomaci, brzina i ubrzanje mehanizama povezivanja i zvučnih talasa tipični su praktični primjeri upotrebe periodičnih funkcija u inženjerskom proračunu.

Fourier raspadanje temelji se na pretpostavci da se sva praktična vrijednost funkcije u intervalu -π ≤x≤ π može izraziti u obliku konvergiranja trigonometrijskih reda (broj se smatra da se konvergiraju ako se sastoji slijed djelomičnih zbirnih zbroja njegovih članova konvergira:

Standardno (\u003d normalno) snimanje kroz iznos SINX i COSX

f (x) \u003d A O + A 1 Cosx + A 2 COS2x + A 3 COS3X + ... + B 1 SINX + B 2 SIN2X + B 3 SIN3X + ...

gdje je o, 1, a 2, ..., b 1, b 2, .. - valjane konstante, tj.

Gdje za raspon od -π do π koeficijenti row FourIer Izračunato formulama:

Koeficijenti A o, A N i B N nazivaju se fourierovi koeficijentiA ako ih mogu naći, tada se zove broj (1) u blizini Fouriera, Odgovarajuće funkcije f (x). Za broj (1), član (1 cosx + b 1 SINX) prvi se zove ili glavni harmoničan

Drugi način za snimanje broja je korištenje ACOSX + BSINX \u003d CSIN omjer (X + α)

f (x) \u003d O + C 1 grijeh (x + α 1) + c 2 grijeh (2x + α 2) + ... + c n grijeh (nx + α n)

Gdje je AO konstanta, c 1 \u003d (a 1 2 + b 1 2) 1/2, s n \u003d (2 + bn 2) 1/2 - amplituda različitih komponenti, a je i je \u003d arctg an / b n.

Za broj (1), član (1 cosx + b 1 SINX) ili C 1 grijeh (X + α 1) naziva se prvim ili glavni harmoničan (A 2 COS2X + B 2 SIN2X) ili C 2 Grijeh (2x + α 2) nazvan drugi harmoničan itd.

Za tačno prezentaciju složenog signala obično je potreban beskonačan broj članova. Međutim, u mnogim praktičnim zadacima dovoljno je razmotriti samo nekoliko prvih članova.

Fourierov niz ne-periodičnih funkcija s periodom od 2π.

Definicija ne-periodičnih funkcija.

Ako je funkcija f (x) je neperiodične, to znači da se ne može rastaviti u Fourierov red za sve vrijednosti x. Međutim, možete definirati niz Fouriera, što predstavlja funkciju u bilo kojem rasponu od 2π širine.

Ako je određena periodična funkcija, možete kreirati novu funkciju, odabir vrijednosti f (x) u određenom rasponu i ponavljajući ih iz ovog raspona s intervalom od 2π. Budući da je nova funkcija periodična s periodom od 2π, može se razgraditi u Fourierovu seriju za sve vrijednosti x. Na primjer, funkcija f (x) \u003d x nije periodična. Međutim, ako je to potrebno da ga razgradi u Fourierov red u intervalu od oko 2π, onda periodična funkcija sa periodom 2π je izgrađen izvan ovog intervala (kao što je prikazano na sl. Dolje).

Za ne-periodične funkcije, poput f (x) \u003d x, zbroj Fourierove serije jednaka je vrijednosti f (x) na svim točkama navedenog raspona, ali nije jednak f (x) za bodove izvan raspona. Da biste pronašli red Fourier ne-periodičke funkcije u rasponu od 2π, Fourierove koeficijenti formula se koristi.

Čak i neparne funkcije.

Kažu funkciju y \u003d f (x) čak iAko f (-x) \u003d f (x) za sve vrijednosti x. Grafike i funkcije su uvijek simetrično u odnosu na os y (i.e. su ogledalo odražava). Dva primjera čak i funkcija: y \u003d x 2 i y \u003d cosx.

Kaže se da je funkcija y \u003d f (x) čudanako f (-x) \u003d - f (x) za sve vrijednosti x. Grafikoni neobičnih funkcija uvijek su simetrično u odnosu na početak koordinata.

Mnoge funkcije nisu ni ni ni čudne.

Dekompozicija u Fourierovoj seriji Cosine.

Fourieroviji serija još periodične funkcije F (x) sa razdobljem od 2π sadrži samo članove sa Cosin (I.E., ne sadrži članove sa sinusom) i mogu uključivati \u200b\u200bstalni član. Otuda,

gde koeficijenti Fourierovog serije

Fourier serija neobične periodične funkcije f (x) s razdobljem od 2π sadrži samo članove sa sinusom (I.E. ne sadrži članove sa kosinusom).

Otuda,

gde koeficijenti Fourierovog serije

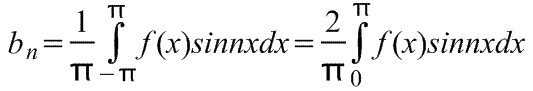
Fourierov red na pola ade.

Ako je funkcija definirana za raspon, recimo od 0 do π, a ne samo od 0 do 2π, može se razgraditi u nizu samo na sinovima ili tolo kosin. Naziva se rezultirajući Fourier serija blizu Fouriera u pola perioda.

Ako želite dobiti raspad Fourier na poluodu kosinusafunkcije F (x) u rasponu od 0 do π, potrebno je napraviti ravnomjerno razdoblje. Na slici. Ispod je funkcija f (x) \u003d x, izgrađena u intervalu iz x \u003d 0 do x \u003d π. Budući da je ravnomjerna funkcija simetrična s obzirom na osovinu f (x), izvedite AB liniju kao što je prikazano na Sl. u nastavku. Ako pretpostavite da je izvan razmatranog intervala, rezultirajući trokutasti oblik je periodičan s periodom od 2π, a zatim konačni raspored ima obrazac, show. Na slici. u nastavku. Budući da je potrebno dobiti četveroierovu raspadanje kosinom, kao i prije, izračunajte Fourierove koeficijente A O i A N

Ako je potrebno za dobivanje fourierov raspadanje na poluvremenu sinova Funkcije f (x) u rasponu od 0 do π, onda je potrebno napraviti čudan periodična funkcija. Na slici. Ispod je funkcija F (x) \u003d x, izgrađena u intervalu od x \u003d 0 do x \u003d π. Budući da je neobična funkcija simetrična u odnosu na početak koordinata, izgrađujemo CD liniju, kao što je prikazano na Sl. Ako pretpostavimo da je izvan razmatranog intervala, rezultirajući rezani signal je periodičan sa periodom od 2π, a zatim konačni raspored ima izgled prikazano na Sl. Budući da je potrebno dobiti raspadanje bijesa na poluvremenu sinova, kao i prije, izračunati Fourierov koeficijent. B.

Fourier serija za proizvoljni interval.

Dekompozicija periodične funkcije s periodom L.

Periodična funkcija F (x) se ponavlja povećanjem x na L, I.E. f (x + l) \u003d f (x). Tranzicija u odnosu na prethodno razgovarali funkcija sa periodom 2π na funkcije s rokom L je prilično jednostavan, jer može biti zamjenom varijable.

Da biste pronašli Fourierovu seriju F (x) u rasponu / 2 2≤x≤l / 2, uvodimo novu varijablu u na takav način da se funkcija F (x) događa 2π u odnosu na U. Ako je u \u003d 2πx / l, tada je x \u003d -l / 2 na U \u003d -π i x \u003d l / 2 na U \u003d π. Takođe pustite f (x) \u003d f (lu / 2π) \u003d f (u). Fourier serija F (u) ima pogled

(Granice integracije mogu se zamijeniti bilo kojim intervalom L dužine, na primjer, od 0 do L)

Fourier serija u poluvremenu za funkcije navedene u intervalu l ≠ 2π.

Za zamjenu U \u003d πh / l, interval iz X \u003d 0 do X \u003d l odgovara intervalu od U \u003d 0 do u \u003d π. Slijedom toga, funkcija se može razgraditi u nizu samo kozinom ili samo u Sinusu, I.E. u fourier serija na pola ADOD-a.

Dekompozicija kosinua u rasponu od 0 do l ima oblik

Jedna od vrsta funkcionalne serije je trigonometrijska serija

Zadatak je odabrati koeficijente serije tako da se konvergira na funkcije date u intervalu [-π, π]; Drugim riječima, potrebno je razgraditi ovu funkciju u trigonometrijskom redu. Dovoljan uvjet rješenja ovog problema je što je funkcija u intervalu [-π, π] komadno-kontinuiranom i komadno diferencirajućom, tj. Tako da interval [-π, π] može podijeliti u konačni broj djelomične Intervali u svakoj od kojih je ova funkcija kontinuirana i ima izveden (na krajevima djelomičnih intervala funkcija mora imati ograničene jednostrane granice i jednostrane derivate, pri izračunavanju funkcije funkcije na kraju djelomičnog Interval, uzima se jednostrana granica). Stanje dijela različitog razlikovanja može se zamijeniti stanjem komadne monotonije funkcije, odnosno zahtjeva da se osigura da je funkcija Monotonne u svakom od djelomičnih intervala. Dovoljni uvjet za raspadanje funkcije u intervalu [-π, π] u trigonometrijskoj seriji je također zahtjev tako da u ovom intervalu funkcija ima ograničenu promjenu. Po definiciji funkcije F (x), postoji ograničena promjena u intervalu ako s bilo kojom particijom ovog intervala na konačni broj intervala

vrijednost

ograničena iznad istog broja.

Sa takvim funkcijama koje se moraju baviti rješenjima praktičnih zadataka.

Prilikom izvođenja bilo koje od tri navedena dovoljni uslovi Funkcija F (x) predstavljena je u intervalu [-π, π] trigonometrijskom blizu, u kojoj su koeficijenti određeni formulama

Sa takvim koeficijentima se naziva trigonometrijski red u blizini Fourierova. Ova serija se konvergira na f (x) na svakoj tački njenog kontinuiteta; Na lom bodovima se konvergira na prosječne aritmetičke lijeve i desne granične vrijednosti, i.e. k, ako je x tačka za jaz (sl. 1); Na granicama segmenta na broj se konvergira.

Slika 1.

Funkcija izražena u blizini Fourierova, postoji periodična funkcija, a samim tim i broj sastavljen za funkciju navedenu na segmentu [-π, π] izlazi iz ovog segmenta na periodični nastavak ove funkcije (Sl. 2).

Slika 2.

Ako je Fourierona funkcija F (x) predstavljena u proizvoljnom intervalu [α, α + 2π] Dužina 2π, zatim koeficijenti reda A 0, AK, BK (Fourierovi koeficijenti) mogu se odrediti navedenim formulama u kojima Granice integracije zamjenjuju α i α + 2π. Općenito, jer u formulama za 0, a k, B K, postoje funkcije s periodom od 2π, integracija se može provesti u bilo kojem intervalu dužine 2π.

Fourier serija može se koristiti za približni prikaz funkcije, naime: funkcija F (x) zamjenjuje se približno jednakim količinom iz iznosa s n (x) prvih nekoliko članova serije Fourierove:

Izraz SN (X), gdje su 0, AK, BK Fourierie koeficijenti F (x), u usporedbi s drugim izrazima iste vrste s istim vrijednostima n, ali s drugim koeficijentima, dovodi do minimalnog prosječnog kvadratnog odstupanja SN (X ) iz f (x), koji je definiran kao

Ovisno o vrsti simetrije funkcije, moguće su neke pojednostavljene. Ako je funkcija čak, i.e. f (-x) \u003d f (x), onda

a funkcija se raspada u nizu kosinusa. Ako su funkcije neparne, i.e. f (-m) \u003d - f (x), onda

a funkcija se raspada u nizu sinusa. Ako funkcija zadovoljava stanje f (x + π) \u003d - f (x), tj. Krivulja koja se odnosi na polovinu segmenta 2π je ogledalo odraz druge polovine krivulje,

Funkcija se može odrediti ne samo na segmentu 2π duge, već i na segmentu bilo koje dužine 2L. Ako zadovoljava gore navedene uvjete u ovom segmentu, postavlja se u Fourierovu seriju sljedećeg tipa:

a koeficijenti broja izračunavaju se formulama

U kartici. 1 Dana Dekompozicija nekih funkcija.

Tabela 1.

Trigonometrijski redak može se snimiti u ovom obrascu:

Funkcija Fourierove serije F (x) Kongurira se u prijevremenu funkciju glatke funkcije. Ako funkcija f (x) i njeni derivati \u200b\u200bf "(x), f" (x), ..., FK -1 (x) su kontinuirani, a F (K) (x) omogućava samo jazničke tačke 1. rod u konačnici, Fourierovi koeficijenti A N, BN Funkcije F (x) bit će

Simbol je označen takva veličina koja

Dekompozicija u trigonometrijski redak naziva se harmoničnom analizom i trigonometrijske funkcijeUključeno u ovu seriju - Harmonics. Izračun komponenti harmonika naziva se harmonična sinteza.

Prilikom izračunavanja struktura često je potrebno raspadati u Fourierovoj seriji razne funkcijedefinirane grafikonima, a prije svega prikazuju teret. U kartici. 2 i 3 dekompozicije daju se za neke funkcije karakteristične za teret, uključujući redove koji odgovaraju koncentriranim silama.

Tabela 2.

Raspored funkcija	Fourier Red	n.

Transkript.

1 Ministarstvo obrazovanja i nauke iz Ruske Federacije Novosibirsk Državno sveučilište Fakultet Fakulteta Fakulteta R. Klepera Ryadov Fourieru u primerima i zadacima Vodič Novosibirsk 211

2 UDC BBK BL161 B44 B44 Belleeva R. K. Fourierov redove u primjerima i zadacima: Tutorial / Novosib. Stanje Un-t. Novosibirsk, str. ISBN Priručnik za studiju postavlja osnovne informacije o redovima Fourieru, postoje primjeri za svaku proučenu temu. Primjer upotrebe Fourierove metode detaljno se rastavlja za rješavanje problema poprečnih oscilacija niza. Daje se ilustrativni materijal. Postoje zadaci za neovisno rješenje. Dizajniran za studente i nastavnike Fizičkog fakulteta NSU-a. Odštampano Odlukom Metodološke komisije Fizičkog fakulteta NSU-a. Recenzent dr. FIZ.-Mat. nauka V. A. Aleksandrov dodatak pripremljen kao deo provedbe programa razvojnog programa NIU-NSU. ISBN C NOVOSIBIRSKI državni univerzitet, 211 C Belleeva R. K., 211

3 1. Razgradnja 2π-periodične funkcije u definiciji Fourierove serije. U blizini Fourierove funkcije F (x) se naziva funkcionalna serija A 2 + (COSNX + BN SIN NX), (1) gdje se "BN koeficijenti izračunavaju koristeći formule: an \u003d 1 π bn \u003d 1 π f (x) COSNXDX, n \u003d, 1, ..., (2) f (x) sin nxdx, n \u003d 1, 2, .... (3) formulas (2) (3) nazivaju se EULER Fouler formule. Činjenica da funkcije f (x) odgovaraju Fourierovoj seriji (1) zabilježene su kao formula f (x) a 2 + (COSNX + BN SIN NX) (4) i kaže se da je desna strana formule (4) je formalni broj Fourier Funkcija F (x). Drugim riječima, formula (4) znači samo da su koeficijenti a n, b n pronađeni formulama (2), (3). 3.

4 Definicija. 2π-periodična funkcija F (x) naziva se komadno glatkom, ako u intervalu [, π] postoji konačan broj bodova \u003d x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4

5 Sl. 1. Funkcija Funkcija F (x) Izračunajte Fourierove koeficijente A \u003d 1 π f (x) dx \u003d 1 π x 2 2 π \u003d π, an \u003d 1 π f (x) cosnxdx \u003d 2 π \u003d 2 () x sin nx cos NX + Π NN 2 \u003d 2 π (1) N 1 N 2 \u003d BN \u003d 1 π π \u003d 2 π f (x) cosnxdx \u003d cos nx cosn n 2 \u003d 4 πn2, sa n neparnima, s n, f (x ) SIN NXDX \u003d, jer je funkcija f (x). Napišemo formalnu Fourier seriju za funkciju F (x): F (x) π 2 4 π K \u003d 5 cos (2k + 1) x (2k + 1) 2.

6 Otkrijte da li je funkcija f (x) komadno glatko. Budući da je kontinuirano, izračunavamo samo granice (6) na konačnim mjestima jaza x \u003d ± π i na mjestu prekida x \u003d: i f (π h) f (π) π h π lim \u003d lim H + HH + H \u003d 1, F (+ H) F (+) + h () lim \u003d lim + hh + h) f (+) + h lim \u003d lim \u003d 1, h + hh + h \u003d 1, f (h) f () h () lim \u003d lim \u003d 1. H + hh + h granice postoje i ograničeni su, pa komad komadno glatka funkcija. Prema teoriji o trenutnoj konvergenciji, njegova Fourierova serija konvergira se na broj f (x) u svakom trenutku, odnosno f (x) \u003d π 2 4 π k \u003d cos (2k + 1) + x (2k + 1) + x (2k + 1) + x (2k + 1) + x (2k + 1) 2 \u003d \u003d π 2 4 (cosx + 19 π cos 3x) cos 5x (7) na slici. 2, 3 prikazuje prirodu aproksimacije djelomičnih suja s Fourierovom serije S n (x), gdje je s n (x) \u003d an 2 + (AK Coskx + BK SIN KX), k \u003d 1 do funkcije f (x ) U intervalu [, π]. 6.

7 Sl. 2. Grafikon funkcije F (x) s djelomičnim iznosima s (x) \u003d 2 i s 1 (x) \u003d A 2 + A 1 cos X je na njemu naložen. 3. Raspored F (x) funkcija sa djelomičnim zbrojem od 99 (x) \u003d A 2 + A 1 COS X + + A 99 COS 99x 7

8 suptera u (7) x \u003d Dobivamo: \u003d π 2 4 π k \u003d 1 (2k + 1) 2, odakle nalazimo zbroj numeričke serije: \u003d π2 8. Upoznavanje ovog reda, jeste Jednostavno pronalazak sljedećeg iznosa: S \u003d () s \u003d () \u003d π, dakle s \u003d π2 6, odnosno 1 n \u003d π suma ovog poznatog reda prvo je pronašao Leonard Euler. Često se nalazi u matematičkoj analizi i njenim primjenama. Primjer 2. Nacrtajte raspored, pronalazimo Fourierovu seriju funkcije određene formule F (x) \u003d x za x< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8

9 Sl. 4. Raspored F (x) funkcija F (x) Funkcija kontinuirano je različita u intervalu (, π). Na bodovima X \u003d ± π, ima ograničenje konačnih (5): F () \u003d, f (π) \u003d π. Pored toga, postoje krajnje granice (6): f (+ h) f (+) lim \u003d 1 i h + hf (π h) f (π +) lim \u003d 1. h + h znači f (x) komadno glatko Funkcija. Budući da je funkcija f (x) neparna, a zatim n \u003d. BN koeficijenti Pronađite integraciju u dijelove: BN \u003d 1 π f (x) sin πnxdx \u003d 1 [x cosntx π πn + 1 n \u003d 1 πn [(1) n π + (1) n π] \u003d 2 (1) n + jedan. n Napravite formalni Fourier seriju funkcija 2 (1) N + 1 F (x) SIN NX. N 9 cosnxdx] \u003d

10 Prema teoriji o trenutnoj konvergenciji komadno glatko 2π-periodične funkcije, Fourier serija F (x) konvergira se na količinu: 2 (1) n + 1 sin NX \u003d N f (x) \u003d x, ako je π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1

11 Sl. 6. Grafikon funkcije F (x) s djelomičnim zbrojem s 2 (x) na njemu naloženi). 7. Raspored F (x) funkcija sa djelomičnim zbrojem s 3 (x) 11 na njoj na njemu.

12 Sl. 8. Grafikon funkcije F (x) s djelomičnim zbrojem od 99 (x) na IT-u, koristite rezultirajuće Fourier seriju da biste pronašli sume dva numerička reda. Stavite u (8) x \u003d π / 2. Zatim 2 () + ... \u003d π 2, ili \u003d n \u003d (1) n 2n + 1 \u003d π 4. Lako smo pronašli zbroj poznatog reda leibitusa. Stavljanje u (8) x \u003d π / 3, pronaći ćemo () + ... \u003d π 2 3, ili (1+ 1) () (k) 3π + ... \u003d 3k

13 Primjer 3. Nacrtajte raspored, pronalazimo Fourierovu seriju funkcije F (x) \u003d SIN X, pretpostavljajući da ima razdoblje od 2π, a 1 izračunavanje zbroja numeričke serije 4N 2 1. rješenje. Funkcija grafikona F (x) prikazana je na slici. 9. Očito, F (x) \u003d SIN X je neprekidno čak funkcioniranje s periodom π. Ali 2π je i funkcija funkcije f (x). Sl. 9. Funkcija funkcije F (x) Izračunajte Fourierove koeficijente. Sve b n \u003d jer je funkcija čak. Iskorištavanje trigonometrijskih formula Izračunajte AT 1: An \u003d 1 π \u003d 1 π SIN X COSNXDX \u003d 2 π SIN X COSNXDX \u003d (Grijeh (1 + n) x grijeh (1 n) x) dx \u003d 1 () π cos (1 + n) x cos (1 n) x + \u003d 2 () 1 + (1) n \u003d π 1 + n 1 n π 1 n 2 (4 1, ako n \u003d 2k, \u003d π n 2 1, ako N \u003d 2k.

14 Ovaj proračun ne dozvoljava da pronađemo koeficijent A 1, jer sa N \u003d 1, nazivnice se nalazi na nulu. Stoga izračunavamo koeficijent A 1 direktno: A 1 \u003d 1 π SIN X CoSXDX \u003d. Od (x) se kontinuirano razlikuje (,) i (, π) i na bodovima KP, (k Integer), postoje krajnje granice (5) i (6), a zatim na njemu na njemu Svaka tačka: \u003d 2 π 4 π SINX \u003d 2 π 4 π cos 2nx 4n 2 1 \u003d (1 1 1 cos 2x cos 4x + 1) cos 6x priroda aproksimacije funkcije f (x) od strane djelomičnih suma Doserba Fourierova je prikazana. (9) Sl. 1. Raspored F (x) funkcija s djelomičnim sumom s (x) 14 napisano na njemu

15 riža 11. Grafikon funkcije f (x) s djelomičnim zbrojem s) s djelomičnom zbrojem od 1 (x) Sl. 12. Grafikon funkcije F (x) s djelomičnim zbrojem s 2 (x) natpisan na njemu). 13. Funkcija Funkcija F (x) s djelomičnim zbrojem od 99 (x) 15 na njemu

16 1 Izračunajte zbroj numeričke serije. Za ovo, 4n 2 1 stavite u (9) x \u003d. Tada CoSNX \u003d 1 za sve n \u003d 1, 2, ... i zato 2 π 4 π 1 4N 2 1 \u003d. 1 4N 2 1 \u003d 1 \u003d 1 2. Primjer 4. Dokazali smo da ako je po dijelovima glatka neprekidna funkcija f (x) zadovoljava uslov F (x π) \u003d f (x) za sve x (i.e. je π-periodične), onda 2n 1 \u003d b 2n 1 \u003d za sve N 1, i obrnuto, ako je 2n 1 \u003d b 2n 1 \u003d za sve N 1, tada je f (x) π-periodične. Odluka. Neka funkcija f (x) bude π-periodična. Izračunajte svoje Fourier koeficijenti A 2N 1 i B 2N 1: \u003d 1 π (A 2N 1 \u003d 1 π F (x) cos (2N 1) XDX + F (X) COS (2N 1) xdx \u003d) F (X) COS (2N 1) XDX. U prvom integralnom, zamijenit ćemo varijablu x \u003d t π: f (x) cos (2n 1) xdx \u003d f (t π) cos (2n 1) (t + π) dt. šesnaest

Svlačenjem na ovaj način da (2n 1) (T + π) \u003d cos (2n 1) t i f (t π) \u003d f (t), dobivamo: 2n 1 \u003d 1 π (f (x) cos ( 2N 1) x DX +) F (x) COS (2N 1) x DX \u003d. Slično tome, dokazuje se da je b 2n 1 \u003d. Naprotiv, neka 2n 1 \u003d b 2n 1 \u003d. Budući da je funkcija F (x) kontinuirana, zatim teoremom na reprezentativnosti funkcije na trenutku u sljedećem Fourieru, tada imamo f (x π) \u003d \u003d f (x) \u003d (2n cos 2nx + b 2N SIN 2NX). (A2N COS 2N (x π) + b 2n sin 2n (x π)) \u003d (A2N COS 2NX + B 2N SIN 2NX) \u003d F (x), što znači da je F (x) je funkcija π-periodične. Primer 5. Dokazujemo da ako komadno nesmetana funkcija f (x) zadovoljava stanje f (x) \u003d f (x) za sve X, zatim a \u003d i 2n \u003d b 2n \u003d za sve n 1 i obrnuto, Ako je a \u003d a 2n \u003d b 2n \u003d, tada je f (x π) \u003d f (x) za sve x. Odluka. Neka funkcija f (x) zadovoljava stanje f (x π) \u003d f (x). Izračunajte svoje Fourierove koeficijente: 17

18 \u003d 1 π (a n \u003d 1 π f (x) cos nxdx + f (x) cosnxdx \u003d) f (x) cosnxdx. U prvom integralnom ćemo zamijeniti varijablu x \u003d t π. Zatim f (x) cosnxdx \u003d f (t π) cosn (t π) dt. Uzimajući taj način cos n (t π) \u003d (1) n cos if (t π) \u003d f (t), dobijamo: an \u003d 1 π ((1) n) F (t) cos DT \u003d, ako N čak, \u003d 2 π f (t) COS NT DT, ako je N neparan. Π Slično tome, dokazuje se da je b 2n \u003d. Naprotiv, neka je a \u003d 2n \u003d b 2n \u003d, za sve n 1. Budući da je funkcija F (x) kontinuirana, zatim teoremom o reprezentaciji, jednakost F (x) \u003d (x) \u003d (2n 1 cos (x) \u003d ) \u003d (A 2N 1 COS (2N 1) X + B 2N 1 SIN (2N 1) X). osamnaest

19 Tada \u003d F (x π) \u003d \u003d \u003d f (x). Primjer 6. Proučavamo kako nastaviti funkciju F (x) integrirana u interval [, π / 2] na interval [, π] tako da njegova Fourierova serija vjeruje: 2n 1 cos (2n 1) x. (1) Odluka. Neka se funkcija grafikon pogleda na slici. 14. Od broja (1) A \u003d A 2N \u003d B 2N \u003d za sve n, zatim iz primjera 5 slijedi da funkcija f (x) mora zadovoljiti jednakosti f (x π) \u003d f (x) za sve x. Ovo zapažanje daje način da se nastavi funkciju f (x) na intervalu [, / 2]: f (x) \u003d f (x + π), sl. 15. Iz činjenice da red (1) sadrži samo kosines, zaključujemo da bi stalna funkcija f (x) trebala biti čak (i.e. njegov raspored trebao bi biti simetričan u odnosu na osovinu o oia), rižu

20 Sl. 14. Funkcija Grafikon F (x) Sl. 15. Raspored za nastavak funkcije f (x) za interval [, / 2] 2

21 Dakle, željena funkcija se gleda na Sl. 16. Sl. 16. Raspored za nastavak funkcije F (x) za interval [, π] Zaključujemo da funkcija treba nastaviti nastavljati na sljedeći način: f (x) \u003d f (x), f (π x) \u003d f ( x), koja je, interval [π / 2, π], graf funkcije f (x) je centralno simetričan u odnosu na tačku (π / 2), a na intervalu [, π], njezin graf je simetrično u odnosu na osovinu OY. 21.

22 Generalizacija primjera 3 6 Neka L\u003e. Razmotrite dva uvjeta: a) f (l x) \u003d f (x); b) f (l + x) \u003d f (x), x [, l / 2]. Sa geometrijskog stanovišta, stanje (a) znači da je grafikon funkcija f (x) simetrična u odnosu na vertikalni direktan X \u003d l / 2, te stanje (b) da je grafikon f (x) centralno simetričan u odnosu na tačku (L / 2;) na osi apscisa. Tada su sljedeće izjave istinite: 1) ako je funkcija f (x) parno (a), a zatim b 1 \u003d b 3 \u003d ... \u003d, a 1 \u003d 3 \u003d a 5 \u003d ... \u003d; 2) ako je funkcija f (x) je čak i stanje (b), tada b 1 \u003d b 2 \u003d b 3 \u003d ... \u003d, a \u003d a 2 \u003d 4 \u003d ... \u003d; 3) ako je funkcija f (x) je čudno i stanja (a) je zadovoljan, a zatim i \u003d a 1 \u003d a 2 \u003d ... \u003d b 2 \u003d b 4 \u003d b 6 \u003d ... \u003d; 4) Ako je funkcija f (x) neobična i uvjetna (b) je zadovoljna, a zatim a \u003d a 1 \u003d a 2 \u003d ... \u003d, b 1 \u003d b 3 \u003d b 5 \u003d ... \u003d. Zadaci u zadacima 1 7 Draw grafikone i pronađite Fourierov red za funkcije (pod pretpostavkom da imaju period od 2π: ako< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22

23 (1, ako / 2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23

24 2. Dekompozicija funkcije navedena u intervalu [, π], samo sinusom ili samo kozinom. Neka funkcija F postavi u intervalu [, π]. Želeći da ga razgradi u ovom jazu u nizu Fourieru, prvo ćemo nastaviti u intervalu [, π nasumično, a zatim koristiti Euler Fouler formule. Arbitrantnost u nastavku funkcije dovodi do činjenice da za istu funkciju f: [, π] r možemo dobiti različite Fourieru reda. Ali možete koristiti ovu arbitrarnost da biste dobili raspadanje samo u sinus ili samo Cosine: U prvom slučaju, dovoljno je da nastavi sa neparnim putem, a u drugom. Algoritam rešenja 1. Nastavite funkciju na neparni (čak) način na (,), a zatim periodično, s periodom od 2π Nastavite funkciju na cijeloj osovini. 2. Izračunajte Fourierove koeficijente. 3. Napravite Fourierovu seriju F (x). 4. Provjerite uvjete za konvergenciju reda. 5. Navedite funkciju kojoj će se ova serija konvergirati. Primjer 7. Raširite funkciju F (x) \u003d cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис

25 Sl. 17. Raspored stalne funkcije očito je da je funkcija f (x) komadno glatko. Izračunajte Fourierove koeficijente: a n \u003d za sve n jer je funkcija f (x) neparna. Ako N 1, zatim BN \u003d 2 π f (x) sin πnxdx \u003d 2 π cosx sin nxdx \u003d 2 π dx \u003d 2 π cos (n + 1) x cos (n 1) x + \u003d π n + 1 n 1 \u003d 1 (1) n (1) n 1 1 \u003d π N + 1 n 1 \u003d 1, ako n \u003d 2 k + 1, (1) n + 1 (n 1) + (n + 1) \u003d π (n + 1) \u003d π (n + 1) (n 1) 2 2N, ako n \u003d 2k. Π n 2 1 na n \u003d 1 u prethodnim proračunima, nazivnik se odnosi na nulu, tako da se koeficijent B 1 izračunava direktno- 25

26: B 1 \u003d 2 π cosx sin xdx \u003d. Obrišit ćemo niz Fourierove funkcije f (x): f (x) 8 π k \u003d 1 k 4k 2 1 sin 2kx. Budući da je funkcija f (x) komadno glatko, zatim prema teoriji detektiv konvergencije, Fourier asortiman F (x) funkcije se konvergira na količinu: cosx, ako je π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26

27 Sl. 18. Grafikon funkcije F (x) s djelomičnim sumom od 1 (x) na njemu se navodi. 19. Raspored F (x) funkcija s djelomičnom zbrojem s 2 (x) 27

28 Sl. 2. Grafikon funkcije F (x) s djelomičnim zbrojem s 3 (x) natpisan na njemu) na slici. 21 prikazuje grafikone funkcije f (x) i njegove djelomične sume s 99 (x). Sl. 21. Raspored F (x) funkcija s djelomičnim zbrojem od 99 (x) 28 na njemu

29 Primjer 8. Neopunjavanje funkcije F (x) \u003d E sjekire, a\u003e, x [, π], u nizu Fourieru samo kosinu. Odluka. Nastavljamo funkciju na ravnomjernom putu (,) (tj. Tako da je jednakost f (x) \u003d f (x) izvedena za sve x (, π)), a zatim periodično s periodom od 2π po numeričkoj osovini . Dobijamo funkciju f (x), čiji je graf predstavljen na Sl. 22. Funkcija F (x) na bodovima Sl. 22. Raspored stalne funkcije F (x) x \u003d kπ, k je cijeli broj, ima lisicu. Izračunajte Fourierove koeficijente: B n \u003d, jer je f (x). Integriranje u dijelove dobivamo 29

30 an \u003d 2 π a \u003d 2 π \u003d 2 COSNXD (e Ax) \u003d 2 πa Ex DX \u003d 2 π a (eaπ 1), f (x) cos πnxdx \u003d 2 π πa eax cosnx \u003d 2 πa (eaπ cossno 1 ) + 2N πa 2 π e AX cos nxdx \u003d + 2n e ax sin nxdx \u003d πa sin nxde ax \u003d 2 πa (eaπ cos n π 1) + 2n π sin nx π a 2eax 2n2 e ax cos nxdx \u003d 2 π a 2 π a (eaπ cos n π 1) n2 aa n. 2 Stoga, n \u003d 2a e aπ cos n π 1. π a 2 + n 2 od F (x) kontinuirano je, zatim prema struji trenutne konvergencije, četverorijskim redom konvergira na F (x). Dakle, za sve x [, π] imamo f (x) \u003d 1 π a (eaπ 1) + 2a π k \u003d 1 e aπ (1) k 1 a 2 + k 2 coskx (x π). Riža pokazuju postepenu približavanje djelomičnih suja Fourierove serije na datu funkciju pucanja. 3.

31 Sl. 23. Grafikoni funkcija F (x) i s (x) Sl. 24. Grafikoni funkcija f (x) i s 1 (x) Sl. 25. Grafikoni funkcija F (x) i S 2 (x) Sl. 26. Grafikoni funkcija f (x) i s 3 (x) 31

32 Sl. 27. Funkcijski grafikoni f (x) i s 4 (x) Sl. 28. Grafikoni funkcija F (x) i s 99 (x) zadaci 9. Istražite funkciju f (x) \u003d cos x, x π, u Fourierovom redu samo kosinus. 1. Istražite funkciju f (x) \u003d e sjekire, a\u003e, x π, u Fourierovoj seriji samo u sinusu. 11. Istražite funkciju F (x) \u003d x 2, x π, u Fourierovoj seriji samo u sinusima. 12. Raširite funkciju F (x) \u003d SIN AX, X Π, u Fourierovoj seriji samo kosinusom. 13. Raširite funkciju F (x) \u003d x SIN X, X Π, u Fourierovoj seriji samo u sinusu. Odgovori 9. CoSX \u003d cosx. 1. E Ax \u003d 2 [1 (1) K E AΠ] K SIN KX. π A 2 + K2 K \u003d 1 11. X 2 2 [π 2 (1) N 1 Π N + 2] N 3 ((1) N 1) SIN NX. 32.

33. Ako a nije cijeli broj, onda siroje 1 cosaπ (1 + 2a cos 2nx) + π a 2 (2n) 2 + 2a 1 + cosaπ cos (2n 1) x π a 2 (2n 1) 2 ; Ako je A \u003d 2m parni broj, a zatim sih 2mx \u003d 8m cos (2n 1) x π (2m) 2 (2n 1) 2; Ako je A \u003d 2m 1 pozitivan neparni broj, a zatim grijeh (2m 1) x \u003d 2 (cos 2nx) 1 + 2 (2m 1). π (2m 1) 2 (2N) π 16 n sin x sin 2nx. 2 π (4N 2 1) 2 3. Fourierov niz funkcija s proizvoljnim razdobljem pretpostaviće da je funkcija f (x) postavljena u intervalu [L, L], L\u003e. Izrađujući zamjenu x \u003d ly, y π, dobivamo funkciju g (y) \u003d f (ly / π), određena u japu π [, π]. Ova funkcija G (y) odgovara (formalnoj) Fourierovoj seriji () Ly F \u003d G (y) A π 2 + (koznik + bn Sin NY), čiji su koeficijenti koji se nalaze prema Euler Fouler Fouler formulas: An \u003d 1 π g (y) Cosny dy \u003d 1 π f (ly π) cos ny dy, n \u003d, 1, 2, ..., 33

34 bn \u003d 1 π g (y) sinny dy \u003d 1 π f () lyn ny dy, n \u003d 1, 2, .... π Povratak u staru varijablu, tj. Vjerujući u pisanu formulate y \u003d πx / l , dobivamo funkciju f (x) trigonometrijska serija nekoliko modificiranih tipa: gdje f (x) a 2 + an \u003d 1 lllll (cos πnx lf (x) cos πnx lf (x) sin πnx l + bn SINX), (11) L DX, N \u003d, 1, 2, ..., (12) DX, N \u003d 1, 2, .... (13) Kaže se da formule (11) (13) određeni su raspadanje u Fourierovoj seriji funkcija sa proizvoljnim periodom. Primjer 9. Pronaći ćemo Fourierovu seriju funkcije navedene u intervalu (L, L) izraza (a, ako l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34

35 A \u003d 1 llf (x) dx \u003d 1 l dx + 1 ll B DX \u003d A + B, LLAN \u003d 1 llf (x) cos πnx l dx \u003d 1 l \u003d 1 ll a cos πnx l \u003d a + b π nlbn \u003d 1 l dx + 1 ll B cos πnx l sin πn \u003d, ako n, ll sin πnx lf (x) sin πnx l dx + 1 ll dx \u003d b sin πnx πnx l \u003d ba (1 cosπn). Πn će napraviti niz Fourierove funkcije f (x): f (x) a + b π (b a od cosπn \u003d (1) n, a zatim n dx \u003d dx \u003d (1 cosπn) sin πnx). l za n \u003d 2k dobivamo B n \u003d B 2K \u003d, s n \u003d 2k 1 b n \u003d b 2k 1 \u003d 35 2 (b a) π (2k 1).

36 Odavde F (x) A + B (BA) π (sin πx + 1 3πx sin + 1 5πx sin + ... l 3 l 5 l Prema teoriji na degeneratenoj konvergenciji, Fourier serija F (x) se konvergira na iznos A, ako L.< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).

37 Sl. 29. Grafikon funkcije F (x) s grafikonima koji su napisani harmonikom S (x) \u003d 2 i s 1 (x) \u003d B 1 Sinx. Za jasnoću grafiku od tri viša harmonika S 3 (x) \u003d b 3 sin 3πx, s l 5 (x) \u003d b 5 sin 5πx l i s 7 (x) \u003d b 7 sin 7πx pomaknut vertikalno up l 37

38 Sl. 3. Grafikon funkcije F (x) s djelomičnim zbrojem od 99 (x) na njemu se navodi. 31. Fragment Sl. 3 na drugoj skali 38

39 Zadaci u zadacima da se razgrade određene funkcije u navedenim intervalima. 14. f (x) \u003d x 1, (1, 1). 15. f (x) \u003d CH2X, (2, 2] f (x) \u003d x (1 x), (1, 1]. 17. f (x) \u003d cos π x, [1, 1] f (x ) \u003d SIN Π x, (1, 1). (2 1, ako 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39

40 18. f (x) \u003d 8 (1) n n sin nπx. π 1 4N (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (l 22. a) f (x) \u003d al 4 2) 1 (4n 2) πx cos, π 2 (2n 1) 2 L b) f (x) \u003d 4al (1) n 1 (2n 1) πx grijeh. π 2 (2n 1) 2 L 23. a) f (x) \u003d (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x ... b) f ( x) \u003d 4 (sin π π 2 2 x 1 3 sin 3π) + 2 2 x (sin π π 2 x cos 2π) 2 x složen oblik serije Fourier raspada F (x) \u003d CNE INX, gdje je CN \u003d 1 2π F (x) E INX DX, N \u003d ± 1, ± 2, ... naziva se složen oblik serije Fouriera. Funkcija se raspada u složenu Fourierovu seriju prilikom obavljanja istih uvjeta pod kojim se raspada u Fourierove realnu seriju. četvoro

41 Primjer 1. Pronađite seriju Fouriera u složenom obliku funkcije navedene formulom F (x) \u003d e sjekirom, u intervalu [, π), gdje je pravi broj. Odluka. Izračunajte koeficijente: \u003d c n \u003d 1 2π f (x) e inx dx \u003d 1 2π e (A in) x dx \u003d 1 ((1) n e aπ (1) n e aπ) \u003d (1) n sh aπ. 2π (A in) π (A in) Kompleks Fourier serija funkcije F ima oblik f (x) sh aπ π n \u003d (1) n a u EINX-u. Uvjeren je da je funkcija f (x) komadno glatko: u intervalu (, π) kontinuirano je različit, a na bodovima x \u003d ± π postoji ograničena granica (5), (6) lim h + ea ( + H) \u003d e aπ, lim h + ea (π h) \u003d e aπ, ea (+ h) ea (+) lim h + h \u003d ae aπ ea (π h) ea (π), lim h + h \u003d Ae aπ. Slijedom toga, funkcija F (x) predstavlja fofier sh aπ π n \u003d (1) n a u EINX-u, koji se konvergira na količinu: (e s (x) \u003d sjekira, ako je π< x < π, ch a, если x = ±π. 41

42 Primjer 11. Pronaći ćemo Fourierovu seriju u kompleksu i stvarnom obliku funkcije koju je pružila formula F (x) \u003d 1 a 2 1 2A Cosx + A2, gdje a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42

43 Podsjetimo da su zbroj beskonačnog geometrijskog napredovanja s nazivom Q (q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43

44 Sada nalazimo Fourierovu seriju u stvarnom obliku. Da biste to učinili, grupisali smo pojmove sa brojevima n i n za n: a n e inx + a n e inx \u003d 2a neinx + e inx jer c \u003d 1, zatim 2 \u003d 2a n cos nx. f (x) \u003d 1 a 2 1 2A cosx + a \u003d a n cosntx. 2 Ovo su Fourier serija u funkciji Real form F (x). Dakle, bez ijednog integralnog, pronašli smo brojne Fourier funkcije. Istovremeno, izračunali smo teški integral, ovisno o parametrima Cos NXDX 1 2A Cosx + A \u003d 2 π A 2 1 A2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44

45 A (ZZ 1) F (x) \u003d 2i (1 A (ZZ 1) + A 2) \u003d I 2 + I (A + A 1) Z 2 2 (ZA) (ZA 1) \u003d \u003d I 2 + I () A 2 ZA + A 1. Za 1 Svaka od jednostavnih frakcija raspadaju se prema formuli geometrijskog napredovanja: + Aza \u003d A 1 Z 1 A \u003d AANZZN, N \u003d za 1 za \u003d AZ \u003d ANZ n. n \u003d Ovo je moguće jer je AZ \u003d A / Z \u003d a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, ili, više kratkih, c n \u003d 1 2i a n sgnn. Dakle, Fourier serija u sveobuhvatnom pronađenom obliku. Grupirao je pojmove sa brojevima n i n, dobijamo niz Fourierovih funkcija u stvarnom obliku: \u003d f (x) \u003d + grijeh x 1 2a cosx + a + 2 (1 2i e inx 1 2i an e inx n \u003d +) \u003d CNE INX \u003d SIN NX. Opet smo uspjeli izračunati sljedeći složeni integral: sin x sin NXDX 1 2A cosx + a 2 \u003d π a 1. (16) 45

46. \u200b\u200bKorištenje (15), izračunajte COS NXDX 1 2A CoSX + A 2 integral za real A, A,\u003e koristeći (16), izračunajte SIN X SIN NXDX integral za Real A, A\u003e A Cosx + A2 u Zadaci, pronađite redove Fourierier u sveobuhvatnom obliku za funkcije. 26. f (x) \u003d sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46

47 5. Ravnopravnost teoreme Ljapunove (Lyapunov jednakost). Neka funkcija F: [, π] r to je takva da F 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47

48 a n \u003d 2 π f (x) cosnxdx \u003d 2 π a cos nxdx \u003d 2 sin na πn. Stoga je jednakost Ljapunov za funkciju f (x) zauzima oblik: 2 a 2 π + 4 sin 2 na \u003d 2a 2 π 2 n 2 π. Od posljednje jednakosti za Π pronalazimo sin 2 na n 2 \u003d a (π a) 2, pretpostavljajući a \u003d π 2, dobivamo sin2 na \u003d 1 na n \u003d 2K 1 i na n \u003d 2k. Shodno tome, k \u003d 1 1 (2k 1) 2 \u003d \u003d π2 8. Primjer 14. Napisat ćemo Lapunov jednakost za funkciju F (x) \u003d x cosx, x [, π] i mi ćemo pronaći sumu Numerički red (4n 2 + 1) 2 (4N 2 1) 4. 1 π rješenje. Direktni proračuni daju \u003d π π f 2 (x) dx \u003d 1 π x 2 cos 2 xdx \u003d 1 π x sin 2xdx \u003d π π x cos x \u003d π x 21 + cos 2x dx \u003d 2 π 1 4π cos 2xdx \u003d

49 Budući da je f (x) ravnomjerna funkcija, a zatim za sve n imamo BN \u003d, AN \u003d 2 π \u003d 1 π 1 \u003d π (n + 1) \u003d f (x) cosnxdx \u003d 2 π 1 cos (n + 1 cos (n + 1) ) x π (n + 1) 2 x cosxcosnxdx \u003d x (cos (n + 1) x + cos (n 1) x) dx \u003d 1 π grijeh (n + 1) xdx grijeh (n 1) xdx \u003d π (n 1) xdx \u003d π (n 1) xdx \u003d π 1) π π 1 + cos (n 1) x \u003d π (n 1) 2 1 (\u003d (1) (n + 1) 1) 1 (+ (1) (n + 1) 1) \u003d π (n + 1) 1) \u003d π (n + 1) 2 π (n 1) 2 () \u003d (1) (n + 1) 1 1 π (n + 1) + 1 \u003d 2 (n 1) 2 \u003d 2 (1) (n + 1) 1 nk π (n 2 1) \u003d π (4k 2 1) 2, ako n \u003d 2k, 2, ako n \u003d 2k + 1. Koeficijent A 1 mora se izračunati odvojeno, jer je u općoj formuli za n \u003d 1 izvučen na nulu. \u003d 1 π a 1 \u003d 2 π f (x) cosxdx \u003d 2 π x (1 + cos 2x) dx \u003d π 2 1 2π 49 x cos 2 xdx \u003d sin 2xdx \u003d π 2.

50 Dakle, Lyapunov jednakost za funkciju F (x) ima oblik: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) \u003d π, odakle nalazimo zbroj numeričkog reda (4N 2 + 1) 2 (4N 2 1) \u003d π π Zadaci 32. Napišite Lyapunov jednakost za funkciju (XF (x) \u003d 2 πx, ako je x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5

51 π (2n + 1) \u003d π sin 2απ 2απ \u003d 2Sin2 απ α 2 π 2 odgovora + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; Sin 2απ 1 2απ \u003d απ n 2 4Sin2 π 2 (Α 2 n 2) 2. 1 π 35. f (x) g (x) dx \u003d CNDN, gdje CN Fourierovi koeficijent 2π funkcije f (x), i koeficijent DN Funkcije G (x). 6. Diferencijacija Fourierove serije Pustite F: R R kontinuirano različita 2π-periodična funkcija. Njena Fourierova serija ima oblik: f (x) \u003d a 2 + (a n cos nx + b n sin nx). Derivat F (x) ove funkcije bit će kontinuirana i 2π-periodična funkcija za koju se može napisati četveroerolni asortiman: f (x) a 2 + (an cos nx + bn sin NX), gdje a, a BN, N \u003d 1, 2, ... Fourierovi koeficijenti f (x). 51.

52 Teorema (o ubijenoj diferencijaciji Fourierove serije). Sa pretpostavkama izvršenim, jednakost A \u003d, a n \u003d NB N, B n \u003d NA N, N 1. Primjer 15. Neka se komadno nesmetana funkcija F (x) neprekidno u intervalu [, π]. Dokazujemo da prilikom obavljanja stanja f (x) DX \u003d, postoji nejednakost 2 DX 2 DX, nazvana nejednakost stakla i provjerite jesu li jednakost u njemu vrši samo za funkcije obrasca F (x) \u003d a Cosx. Drugim riječima, nejednakost Steklova daje uvjete, prilikom obavljanja malosti izvedenog (u RMS-u) slijedi malost funkcije (na srednjoj srednjoj tvari). Odluka. Nastavit ćemo funkciju f (x) za interval [,] ravnomjerno. Označite kontinuirana funkcija istog simbola f (x). Tada će kontinuirana funkcija biti kontinuirana i komadno glatka na segmentu [, π]. Budući da je funkcija F (x) kontinuirana, tada je F 2 (x) kontinuirano na segmentu i 2 DX< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52

53 Budući da je stalna funkcija čak, tada B n \u003d, a \u003d pod uvjetom. Shodno tome, Ljapunovska ravnopravnost uzima oblik 1 π 2 dx \u003d a 2 π n. (17) Zaključeno je da se za F (x) zaključivanje teoreme o neimaginalnom razlikovanju Fourierove serije zaključuje, odnosno da je \u003d, a \u003d nb n, bn \u003d na n, n 1. Neka Derivat F (x) podvrgava se pauzama na bodovima x 1, x 2, ..., x n u intervalu [, π]. Označavaju x \u003d, x n + 1 \u003d π. Podijelimo interval integracije [, π] na N +1 GAP (X, X 1), ..., (x N, x N + 1), na svakom od kojih je F (x) kontinuirano različit. Zatim, koristeći svojstvo aditivnosti integralnog, a zatim integrirajući u dijelove, dobivamo: BN \u003d 1 π \u003d 1 π \u003d 1 π f (x) sin nxdx \u003d 1 π NF (x) sin nx j \u003d nf ( x) SIN NX J \u003d XJ + 1 XJX J + 1 XJNN Π NJ \u003d XJ + 1 XJX J + 1 XJF (X) SIN NXDX \u003d F (x) cosnxdx \u003d f (x) cosnxdx \u003d \u003d 1 π [(f ( x 1) SIN NX 1 F (x) SIN NX) + + (F (x 2) Sinnx 2 F (x 1) Sin NX 1)

54 + (F (x N + 1) SIN NX N + 1 F (x N) SIN NX N)] na n \u003d 1 π na n \u003d \u003d 1 π na n \u003d na n. x J + 1 A \u003d 1 f (x) dx \u003d 1 n f (x) dx \u003d π π π j \u003d xj \u003d 1 n x j + 1 f (x) π \u003d 1 (f (π) f ()) \u003d. X J Π J \u003d Posljednja jednakost se odvija zbog činjenice da je funkcija F (x) nastavljena ravnomjerno, pa je f (π) \u003d f (). Slično tome, dobivamo n \u003d nb n. Pokazali smo da je teorema na diferencijaciji obnove Fourierove serije za kontinuirano komadno glatku 2π-periodičnu funkciju, čiji je derivat u intervalu [, π] podvrgnut prvim vrstama. Pa f (x) a 2 + (cosntx + bn sin nx) \u003d (na n) sin nx, kao a \u003d, a \u003d nb n \u003d, bn \u003d na n, n \u003d 1, 2, .... od tada 2 dx.< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)

55 Budući da je svaki član reda u (18) veći ili jednak odgovarajućem članu reda u (17), a zatim 2 DX 2 DX. Podsjetivši da je f (x) čak i nastavak izvorne funkcije, imamo 2 DX 2 DX. Što dokazuje jednakost Steklov. Sada istražimo za koje funkcije u nejednakosti Steklova postoji jednakost. Ako je barem za jedan n 2, koeficijent A N razlikuje se od nule, a zatim 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55

56 Zadaci 37. Neka se komadno nesmetano funkcionira f (x) u intervalu [, π]. Dokažite da prilikom izvođenja uvjeta f () \u003d f (π) \u003d, postoji nejednakost 2 DX 2 DX, koja se naziva i nejednakost staklene posuđe i provjerite jesu li jednakost u njemu odvija samo za funkcije obrasca F (x) \u003d b sin x. 38. Neka funkcija F kontinuirana u intervalu [, π] i ima u njemu (s izuzetkom konačnog broja bodova) izvedena f (x) integrirana s kvadratom. Dokažite da ako su uslovi f () \u003d f (π) i f (x) dx \u003d su zadovoljni, tada postoji nejednakost 2 DX 2 DX, koja se naziva nejednakost višnja, a jednakost u njemu se odvija samo za funkcije forme f (x) \u003d cosx + b sin x. 56.

57 7. Upotreba Fourierove serije za rješavanje diferencijalnih jednadžbi u privatnim derivatima u istraživanju stvarnog objekta (fenomen prirode, proizvodnog procesa, upravljačkih sistema itd.) Dva faktora su neophodni: nivo akumuliranog znanja o objektu Prema studiranju i stepenu razvoja matematičkog aparata. Na sadašnjoj fazi naučnog istraživanja, sljedeći lanac je razvijen: fizički model matematičkog modela. Fizička formulacija (model) zadatka je sljedeća: Uvjeti za razvoj procesa i glavnih faktora koji utječu na njega otkrivaju se. Matematička formulacija (model) je opisati faktore odabrane u fizičkoj formulaciji u obliku sistema jednadžbi (algebarskog, diferencijalnog, integralnog itd.). Zadatak se naziva pravilno postavljeno ako u određenom funkcionalnom prostoru postoji rješenje problema, jedini i kontinuirani ovisi o početnim i graničnim uvjetima. Matematički model nije identičan objektu koji se razmatra, ali je njegov približni opis izlaza jednadžbe labavih sitnih poprečnih oscilacija niza slijedit će udžbenik. Neka su krajevi žica fiksni, a sam niz je čvrsto. Ako donesete niz iz ravnotežnog položaja (na primjer, za odlaganje ili udaranje), niz će započeti 57

58 Fluktuacija. Pretpostavljamo da se sve tačke niza pomiču okomito na ravno ravnotežnu poziciju (poprečne oscilacije), a u svakom trenutku se naizi u istoj ravnini. Unesite u ovaj avion Xou pravokutni koordinatni sustav. Zatim, ako je u početnom trenutku T \u003d String je bio smješten duž osi Ox, tada bi vam značilo otklonjenje niza iz ravnotežne pozicije, odnosno položaja tačke niza sa apsisom x u proizvoljni trenutak t odgovara funkciji u (x, t). Uz svaku fiksnu vrijednost t, funkcija grafikona u (x, t) predstavlja oblik oscilirajućeg niza u vrijeme T (Sl. 32). Sa stalnom vrijednošću x, funkcija U (x, t) daje zakon kretanja tačke sa apscisom x duž ravne, paralelne OU osi, derivat Ut brzini ovog pokreta, a drugi izvedeni 2 U T2 ubrzanje. Sl. 32. Sile se primjenjuju na beskonačno male dio žica bit će jednadžba na koju funkcija u (x, t) mora zadovoljiti. Da bismo to učinili, napravit ćemo još pojednostavljenju pretpostavki. Razmotrit ćemo niz apsolutno snage - 58

59 Koy, odnos, pretpostavit ćemo da se niz ne opire savijanjem; To znači da su stres koji proizlaze u nizu uvijek čiji na za cilj tangenta svog trenutnog profila. Pretpostavlja se da niz bude elastičan i pretilski zakon grla; To znači da je promjena u veličini napetosti srazmjerna promjeni u dužini niza. Pretpostavljamo da je niz homogena; To znači da je njegova linearna gustina ρ konstantna. Zanemarujemo vanjske sile. To znači da razmatramo besplatne oscilacije. Proučavat ćemo samo male gudačke fluktuacije. Ako odredite φ (x, t) ugao između osi apscisne osi i tangenta na nizu na apscisskoj točki x u vrijeme T, stanje oscilacija je zbog vrijednosti φ 2 (x, t) može biti Zanemareno u usporedbi s φ (x, t), I.E. φ 2. Budući da je ugao φ mali, a zatim cosφ 1, φ sin φ tg φ u je da se vrijednost (UXX,) 2 također može zanemariti. Odavde odmah slijedi da u procesu oscilacija možemo zanemariti promjenu dužine bilo kojeg niza. Zaista, dužina niza m 1 m 2, koja je dizajnirana za apscisnu jaz u osi, gdje je x 2 \u003d x 1 + x jednak L \u003d x 2 x () 2 u DX X. x Pokazujemo da će s našim pretpostavkama vrijednost napetosti sile biti konstantna duž cijelog niza. Uzmite za ovaj dio niza m 1 m 2 (Sl. 32) u vrijeme t i zamjena djelovanja odbačenog dijela - 59

60 komada napetosti snage T 1 i T 2. Otkad se pod uvjetom svi niz kreću paralelno s OU osi, a vanjske sile nedostaju, zbroj projekcija zateznih sila na osi Ox-a trebaju biti nula: T 1 cosφ (x 1, t) + t 2 cosφ (x 2, t) \u003d. Odavde, zbog malosti uglova φ 1 \u003d φ (x 1, t) i φ 2 \u003d φ (x 2, t), zaključujemo da t 1 \u003d t 2. označava ukupnu vrijednost t 1 \u003d t 2 Kroz T. Sada izračunavamo količinu projekcija f u istim silama na OU osovini: f u \u003d t sin φ (x 2, t) t sin φ (x 1, t). (2) Otkad za sitne uglove sin φ (x, t) tg φ (x, t) i tg φ (x, t) u (x, t) / x, zatim jednadžba (2) može se prepisati tako f u t (TG φ (x 2, t) tg φ (x 1, t)) (u tx (x 2, t) u) x (x 1, t) xx t 2 ux 2 (x 1, t) x. Od tačke X 1 je odabrano proizvoljno, zatim f u t 2 u x2 (x, t) x. Nakon što se nalaze svi sile koje djeluju na odjeljku M 1 m 2, na njega ćemo se primijeniti drugi Newtonski zakon, prema kojem je proizvod mase za ubrzanje jednak zbroju svih tekućih snaga. Masa niza m 1 m 2 je m \u003d ρ ρ ρ x, a ubrzanje je 2 u (x, t). Newton jednadžba t 2 uzima oblik: 2 u t (x, t) x \u003d u 2 α2 2 x2 (x, t) x, gdje je α 2 \u003d t ρ stalan pozitivan broj. 6.

61 Rezanje na x, dobivamo 2 u t (x, t) \u003d u 2 α2 2 x2 (x, t). (21) Kao rezultat toga, dobili smo linearnu homogenu diferencijalnu jednadžbu s privatnim derivatima drugog reda sa stalnim koeficijentima. Naziva se jednadžba nizova ili jednodimenzionalna val jednadžba. Jednadžba (21) u suštini je preformuliranje Newtonovog zakona i opisuje pokret niza. Ali u fizičkoj formulaciji zadatka, zahtjevi su bili prisutni da je kraj žica fiksni i položaj niza u neko vrijeme je poznat. Ovi uvjeti će biti zabilježeni ovim uvjetima: a) Pretpostavit ćemo da su krajevi žica fiksirani na bodovima X \u003d i X \u003d l, tj. Za sve t, omjere u (, t) \u003d, u (, t) \u003d, u ( L, T) \u003d; (22) Pretpostavit ćemo da u vrijeme T \u003d položaj niza poklapa s grafikonom Function F (x), tj. Pretpostavljamo da je jednakost u (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f (x,) \u003d f ( x); (23) B) Pretpostavit ćemo da se u vrijeme T \u003d tačka niza sa apsisom x dat brzina g (x), i.e. Pretpostavit ćemo da u (x,) \u003d g (x). (24) T omjeri (22) nazivaju se graničnim uvjetima, a odnosi (23) i (24) nazivaju se početni uvjeti. Matematički model labavog malog poprečnog poprečnog 61

Koljina na nizu je rješavanje jednadžbe (21) s graničnim uvjetima (22) i početnim uvjetima (23) i (24), rješenje jednadžbe slobodnih poprečnih oscilacija niza Fourierovom metodom rješavanja jednadžbe Jednadžba (21) na terenu x l,< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. Zamjena (25) u (21), dobivamo: x T \u003d α 2 x t, (26) ili t (t) α 2 t (t) \u003d x (x) x (x). (27) Kažu da se dogodilo razdvajanje varijabli. Budući da X i T ne ovise jedni o drugima, lijeva strana u (27) ne ovisi o x, a desno iz t i ukupne vrijednosti tih odnosa 62

63 treba biti trajno, koje označava λ: t (t) α 2 t (t) \u003d x (x) x (x) \u003d λ. Odavde dobijamo dva obična diferencijalne jednadžbe: X (x) λx (x) \u003d, (28) t (t) α 2 λt (t) \u003d. (29) U ovom slučaju granični uvjeti (22) će uzeti oblik x () t (t) \u003d i x (l) t (t) \u003d. Budući da se moraju izvoditi za sve T, T\u003e, a zatim x () \u003d x (l) \u003d. (3) Pronalazimo rješenja jednadžbe (28) koja zadovoljava granične uvjete (3). Razmotrite tri slučaja. Slučaj 1: λ\u003e. Označava λ \u003d β 2. jednadžba (28) uzima oblik x (x) β 2 x (x) \u003d. Njegova karakteristična jednadžba k 2 β 2 \u003d ima korijene k \u003d ± β. Otuda, zajednička odluka Jednadžbe (28) ima oblik x (x) \u003d c e βx + de βx. Moramo odabrati konstantnu C i D tako da se poštuju granični uvjeti (3), I.E. x () \u003d c + d \u003d, x (l) \u003d c e βl + de βl \u003d. Od β, ovaj sistem jednadžbi ima jedno rješenje c \u003d d \u003d. Shodno tome, X (x) i 63

64 u (x, t). Dakle, u slučaju 1 dobili smo trivijalnu odluku, koju nećemo dalje razmotriti. Slučaj 2: λ \u003d. Zatim jednadžba (28) uzima obrazac X (x) \u003d i njegovo rješenje očito je definirano formulom: x (x) \u003d c x + d. Zamjena ovog rješenja u graničnim uvjetima (3), dobivamo x () \u003d d \u003d i x (l) \u003d CL \u003d, to znači c \u003d d \u003d. Slijedom toga, x (x) i u (x, t), a opet smo dobili trivijalno rješenje. Slučaj 3:<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64

65 U budućnosti ćemo dati n samo pozitivne vrijednosti n \u003d 1, 2, ... jer s negativnim n, rješenja tog (vrste. Nπ) λ n \u003d nazivaju se vlastitim brojevima i Funkcije XN (x) \u003d c n sin πnx sa vlastitim funkcijama diferencijalne jednadžbe (28) s graničnim uvjetima (3). Sada riješimo jednadžbu (29). Za to karakteristična jednadžba ima oblik k 2 α 2 λ \u003d. (32) L 2 Otkad smo saznali da su ne-trivijalna rješenja X (x) jednadžbi (28) dostupna samo za negativne λ, jednake λ \u003d n2 π 2, tada ćemo razmotriti takav λ. Korijeni jednadžbe (32) su K \u003d ± I α, a rješenja jednadžbe (29) imaju obrazac: T n (t) \u003d a n sin πnαt + b n cos πnαt, (33) l gdje je a n i b n proizvoljna konstanta. Zamjena formula (31) i (33) u (25), naći ćemo privatna rješenja jednadžbe (21) koja zadovoljavaju ivice (22): ((UN (X, T) \u003d BN cos πnαt + sin πnααt) cn sin ΠNX. Upoznat ću multiplikator c n u nosač i uvođenjem oznaka c n a n \u003d bn i b n c n \u003d an, pišu UN (x, t) u obliku (un (x, t) \u003d an cos πnαt + bn sin πnαt) sin πnαt) . (34) l L 65

66 String Fluktuacije koje odgovaraju rješenjima u n (x, t) nazivaju se vlastitim gudačkim fluktuacijama. Budući da su jednadžba (21) i granični uslovi (22) linearni i homogen, zatim linearna kombinacija rješenja (34) (u (x, t) \u003d an cos πnαt + bn sin πnαt) sin πnx (35) će biti riješen Jednadžbama (21) zadovoljavajuće granične uslove (22) s posebnim odabirom koeficijenata An i BN, koji osigurava jedinstvenu konvergenciju reda. Sada ćemo sad odabrati koeficijente i BN rješenja (35) tako da zadovoljava ne samo graničnu, već i početne uvjete (23) i (24), gdje su F (x), G (x) određene funkcije (i F ( ) \u003d f (l) \u003d g () \u003d g (l) \u003d). Vjerujemo da funkcije f (x) i g (x) zadovoljavaju uslove razgradnje u Fourierovoj seriji. Zamjena u (35) vrijednost t \u003d, dobivamo u (x,) \u003d a n sin πnx l \u003d f (x). Razlikovanje serije (35) t i zamjena t \u003d, dobivamo ut (x,) \u003d πnα bn sin πnx l l \u003d g (x), a ovo je raspadanje funkcija f (x) i g (x) u The Fourierove serije. Stoga je n \u003d 2 l l f (x) sin πnx l dx, b n \u003d 2 l g (x) sin πnx dx. Πnα l (36) 66

67 Zamjena ispitivanja Željela A N i B N u nizu (35) Dobivamo rješenje jednadžbe (21) koja zadovoljava granične uvjete (22) i početne uvjete (23) i (24) i (24). Dakle, riješili smo problem slobodnih sitnih poprečnih vibracija niza. Saznajte fizičko značenje EigenFunctions u N (X, T) zadaci slobodnih fluktuacija žica definiranih formulom (34). Prepisujemo ga u obliku gdje u n (x, t) \u003d α n cos πnα l α n \u003d a 2 n + b2 n, (t + δ n) sin πnx, (37) πnα δ n \u003d arctg b n. L A N od formule (37) pokazuje da sve točke niza čine harmonične oscilacije s istom frekvencijom ω n \u003d πnα i πnα δ n faza. Amplituda oscilacije ovisi o L l apscisa X tačke niza i jednak je α n sin πnx. Sa takvim oscilacijama, sve točke niza istovremeno dopiru do maksimalne devijacije u jednom smjeru ili drugoj i istovremeno prolaze ravnotežni položaj. Takve oscilacije nazivaju se stalnim talasima. Stojeći val će imati N + 1 još uvijek određena korijenima Jednadžbe Sin ΠNX \u003d u intervalu [, L]. Fiksne tačke se nazivaju stalnim talasnim čvorovima. U sredini između čvorova postoje bodovi u kojima odstupanja dostignu maksimum; Takve se tačke nazivaju puffs. Svaki niz može imati vlastite oscilacije strogo definiranih frekvencija ω n \u003d πnα, n \u003d 1, 2, .... ove frekvencije nazivaju se vlastitim nijansima. Najniži l ton koji može proizvesti žice određuje se 67

68 Niska vlastiti frekvencija ω 1 \u003d π t i naziva se glavni ton niza. Preostali tonovi koji odgovaraju L ρ frekvencijama ω n, n \u003d 2, 3, ... nazivaju se obramstoni ili harmonike. Za jasnoću, pokazat ćemo tipične stručke profile, emitiranjem osnovnog tona (Sl. 33), prvi Oberton (Sl. 34) i drugi Oberton (Sl. 35). Sl. 33. Profil gudanja, objavljivanje osnovnog tona. 34. Profil gudanja objavljivanje prvog opernog riže. 35. Profil stringa objavio je drugi Obton ako niz vrši besplatne oscilacije određene početnim uvjetima, čini se da je funkcija u (x, t) viđena iz formule (35), kao zbroj pojedinačnih harmonika. Dakle, proizvoljna fluktuacija 68

69 žica je superpozicija stalnih talasa. Istovremeno, priroda niza (ton, snaga zvuka, timbre) ovisit će o omjeru između amplitude individualne harmoničke sile, visine i glasa zvuka oscilirajućeg niza uzbuđuje fluktuacije Zrak, percipiran ljudskim uhom kao zvuk, koji je objavio niz. Snaga zvuka karakteriše energija ili amplituda oscilacija: veća energija, veća snaga zvuka. Visina zvuka određena je njenom frekvencijom ili razdoblje oscilacija: veća frekvencija, to je veći zvuk. Zvučni timbre određuje se prisustvom pregleda, distribucijom energije harmonikom, I.E., metoda uzbuđenja oscilacija. Amplitude overtona, generalno govoreći, manje amplitude glavnog tona, a Operton faze mogu biti proizvoljne. Naše uho nije osjetljivo na fazu oscilacije. Uporedite, na primjer, dvije krivulje na slici. 36 posuđeno od. Ovo je snimanje zvuka s istim glavnim tonom izvađenim od klarineta (a) i klavira (B). Oba zvuka ne predstavljaju jednostavne sinusoidne oscilacije. Glavna frekvencija zvuka u oba slučaja je ista i stvara isti ton. Ali crteži krivulja su različiti jer se na glavni ton primjenjuje različite Obihhon. U određenom smislu, ovi crteži pokazuju šta je Timbre. 69.

Jednadžbe hiperboličkog tipa. Oscilacije beskrajnog i polu-beskonačnog niza. Fourierona metoda Fourier metoda Stoji valovi 4 Predavanje 4.1 Jednadžbe hiperboličkog tipa. Oscilacije beskrajne i polu-beskonačne

Moskovsko državno tehničko univerzitet civilnog zrakoplovstva V.M. Lyubimov, E.A. Zhukova, V.A. Wokova, yu.a. Shurinov ma t E m a t i k a r i objavljuje za proučavanje disciplina i uslova

Ministarstvo prosvjete i nauke Rusije Federalna državna budžetska obrazovna ustanova visokog stručnog obrazovanja Mati Ruski državni tehnološki univerzitet nazvan po K. E. Tsiolkovskom

Ministarstvo obrazovanja Republike Bjelorusije UO "Vitebsk državno tehnološko univerzitet". "Redovi" Odjela za teorijsku i primijenjenu matematiku. Razvio DC. E.B. Dunin. Održavanje

Federalna agencija za obrazovanje Federalno državno obrazovna ustanova visokog stručnog obrazovanja Južni savezni univerzitet R. M. Gavrilova, G. S. Kostotskaya metodički

Tema praktičnog zanimanje Fourierove serije Fourierove serije za ortogonalne sisteme funkcija Prostor komadno kontinuirane funkcije Generalizirani Bessel nejednakosti i konvergencije Fourierove serije

Teorija serije Teorija serija je bitan dio matematičke analize i pronalazi teorijske i brojne praktične primjene. Postoje brojne numeričke i funkcionalne.

Sadržaj Fourieri redovi 4 Koncept periodične funkcije 4 trigonometrijski polinom 6 3 TRIGONONOMETRIC Fourier Ransles 3 5 Foerierov red za čak i neparne funkcije 6 6 raspada

Federalna agencija za obrazovanje Moskovska državna univerzitet za geodeziju i kartografiju (Miigaik) metodička uputstva i zadaci za samostalni rad po stopi viših matematičkih numeričkih

Predavanje 4. Harmonična analiza. Periodične funkcije Fourierove serije. Harmonična analiza u nauci i tehnologiji često se moraju baviti periodičnim pojavama, tj. Koje se ponavljaju

TOPIC V serija Fourierona predava 6 Dekompozicija periodične funkcije u nizu Fourieru mnogih procesa koji se javljaju u prirodi i tehnologiji imaju svojstva za ponavljanje nakon određenih intervala takvih procesa

Metodičke smjernice za dodjele namire po stopi viših matematike "Obične diferencijalne jednadžbe serije dvostrukog integrala" Dio Š Tema redova Sadržaj redova numeričkih redova konvergencije i divergencije

6 Fourierova reda 6 ortogonalne funkcije Fourierovih funkcija na ortogonalnom sistemu funkcija funkcije φ () i ψ () definirani i integrirani na segment [], nazivaju se ortogonalnim u ovom segmentu ako

Određeni integralni. Integralni zbrojevi i određeni integralni puštaju funkciju y \u003d f (), definirana na segmentu [, b], gdje se daje< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных

5 redova snage 5 Redovi: Definicija, regija Region Funkcionalni red (A + A) + A () + K + A () + K A) (, (5) Gdje, A, A, K, A, k Neki brojevi nazivaju se moćan broj

Bjeloruski Državni univerzitet Primjena primijenjenog matematičkog fakulteta za matematiku i informatiku Viši matematički obrazovni i metodički priručnik za studente Fakulteta primijenjenih matematika i informatike

Razmotrite nekoliko primjera. Primjer. Pronaći ćemo zbroj beskonačnog geometrijskog napredovanja formule Generalnog člana ove serije A + AQ + ... + AQ N + ... (a). a n \u003d aq n. Izračunati svoje djelomične izrege. Ako Q \u003d, onda

Zadatak 1.1. Pronađite u navedenom regionu različitu od identičnih nulta rješenja y \u003d y (x) diferencijalne jednadžbe koja zadovoljava navedene granične uvjete (zadatak Sturm Liouville) rješenja: razmotriti

Predmet matematičke analize: određeni integral neshvatljivih integrala predavača Pakhomova e.g. 2017 Poglavlje II. Određeni integralni i njegova primjena 1. određeni integralni i njegova svojstva 1. Zadaci,

Predavanje 8 4 Zadatak Sturm Liouvillea razmatra se početni granični problem za različitu jednadžbu u drugoj narudžbi Djelomični derivati \u200b\u200bkoji opisuju male poprečne fluktuacije niza string niza

Objašnjenje teksta: znak se čita kao "ekvivalent" i ukazuje da jednadžbe desno od znaka i lijevo od znaka postavlja set rješenja, poklapaju se, znak IR-a ukazuje na različite real brojeve, prijavite se

82 4. ODELJAK 4. Funkcionalni i električni redovi 4.2. Lekcija 3 4.2. Lekcija 3 4.2 .. Dekompozicija funkcije u nizu taylor definicije 4.2 .. Pretpostavimo da je funkcija y \u003d f (x) beskonačno različita u nekoj okolini

Ministarstvo prosvjete i nauke o Rusiji Federalnoj državnoj budžetskoj obrazovnoj ustanovi visokog stručnog obrazovanja "Samara Državni tehnički univerzitet" K a f e d r a primijenjena matematika

Federalna agencija za železničke prevoze URal Državni univerzitet za komunikacije Odjel Odjeljenja "Viša i primijenjena matematika" N. P. Chuev harmonični elementi analize metodički

Predavanje 3 Taylorovi redovi i Maclorena primjena moći redama raspadanje funkcija u redove snage serije Taylor i Maclorena za aplikacije važno je moći razumjeti ovu funkciju u retku za napajanje, te funkcije

C Lavrenchenko wwwwrckoru predavanje Fourierova transformacijski koncept integralne metode transformacije integralnih transformacija Jedna od moćnih metoda matematičke fizike je moćno rješenje

Integriljivost funkcije (od strane Riemanna) i specifičnih integralnih primjera rješavanja problema 1. Konstantna funkcija F (x) \u003d C je integrirana na, jer za bilo koju particiju i bilo koji izbor bodova ξ Inačim

Racem, zadatak. Dokažite da je funkcija Riemanna, ako je 0, m M R (), ako je m, m 0 i frakcija poremećaj, 0, ako neracionalno, prekidaju se u svakoj racionalnoj točki i neprekidno je u svakom iracionalnom mjestu i neprekidno je u svakom iracionalnom mjestu. Odluka.

1 2 Sadržaj 1 Fourierov redovi 5 1.1 Trigonometrijska serija Fourier ............ 5 1.2 Samo Sin & Cos ... .. 7 1.3 Fourier serija u složenom obliku ........... 11 1,4 f (x) \u003d ck? ..................... .....

Jednadžbe matematičke fizike 1. Diferencijalne jednadžbe sa privatnim derivatima Jednadžba koja povezuje nepoznatu funkciju u (x 1, x 2, ..., x n), neovisne varijable x 1, x 2, ..., x n i privatno

Predavanje 4. Val jednadžbe 1. Zaključak ekvivacije oscilacije 2. Jednadstvo uzdužnih oscilacija štapa 3. Početni uvjeti, granični uvjeti 4. Postavljanje zadataka 1. Izlaz jednadžbe za oscilaciju niza

1. Elektrostatika 1 1. Elektrostatika Lekcija 6 Odvajanje varijabli u kartezijskim koordinatama 1.1. (Zadatak 1.49) Z \u003d avion se napuni gustoćom Σ (x, y) \u003d σ grijeh (αx) grijeh (βy), gdje su Σ, α, β stalni.

Modul Predmet Funkcionalne sekvence i serija Svojstva ujednačene konvergencije sekvenci i serijalnih redova Relaci Predavanje Definicija funkcionalnih sekvenci i redaka

Jednadžbe paraboličnog tipa. Način razdvajanja varijabli Problem homogene granične vrijednosti Funkcija izvora Heterogena jednadžba termičke provodljivosti 7 Predavanje 7,1 od jednadžbi paraboličnog tipa. Metoda razdvajanja

Predavanje Numerički redovi Znakovi konvergencije Numeričke serije znakovi konvergencije beskonačno izražavanje numeričkog slijeda + + + + sastavljenog od članova beskrajne, nazivaju numerički broj,

35 7 TRIGONONONOMETRIC Fourier serija Fourierova reda za periodične funkcije s periodom T. Neka F (x) bude komadno - kontinuirana periodična funkcija s periodom T. Razmotrite glavni trigonometrijski sistem

Metalurški fakultet za višu matematiku redovi metodička uputstva Novokuznetsk 5 Federalna agencija za obrazovanje Državno obrazovna ustanova visokog stručnog obrazovanja

Odjel za matematiku i informatiku elementi višeg obrazovnog i metodičkog kompleksa matematike za studente CPA, studenti koji koriste diferencijalni prevodilac modula udaljenih tehnologija:

9. Predsednički i neodređeni integral 9 .. Pretpostavimo u intervalu I R set Function F (). Funkcija F () naziva se primitivna funkcija f () u intervalu I, ako f () \u003d f () za bilo koji i primitivni

Diferencijacija funkcija jednog varijabilnog koncepta izvedenog, njenog geometrijskog i fizičkog značenja problema što rezultira konceptom derivata određivanja tangencijalnih s do linije A x; f (

Jednadžbe hiperboličkog tipa. Oscilacije beskrajnog i polu-beskonačnog niza. Način dalamber beskonačnog niza. Polu-infinite niz formula dalamber 3 Predavanje 3.1 Jednadžbe hiperboličkog tipa.

Sadržaj Uvod. Osnovni pojmovi .... 4 1. Integralne jednadžbe Volterry ... 5 Opcije za domaće zadatke .... 8 2. Otvor za volterra integralnu jednadžbu. 10 domaćih zadataka .... 11

Redovi. Numerički redovi. Glavne definicije imaju beskonačan niz brojeva izražavanja (beskonačna suma) a, a 2, ..., a n, ... a I \u003d A + A 2 + + A N + ... () i \u003d nazvan numeričkim. Brojevi

8. Power redovi 8 .. Funkcionalna serija oblika C N (z) n, (8.) n \u003d gdje se C n numerički slijed, r fiksni broj i z r nazivaju snagom zajedno s c n koeficijentima. Zamjenom varijabli

~ ~ Neodređeni i specifičan integralni koncept primitivnog i neodređenog integralnog. Definicija: Funkcija F naziva se primitivno u odnosu na F funkcije ako su ove funkcije povezane sa sljedećim

3724 reda višestrukih i krivućinskih integrala 1 radnog programa odjeljka "Redovi višestrukih i krivućih integrala" 11 numeričkih redova Koncept numeričke serije numeričkih redaka potreban znak konvergencije

Jedite. Ruda matematička analiza. Numerička i funkcionalna serija Novosibirsk 200 2 Mino zaštita Rusije Gou VPO "Novosibirsk državni pedagoški univerzitet" E.M. Ruda matematička analiza.

Predavanje n 7. Snažna serija i serija Taylor .. zatim reda ..... brojne taylor .... 4. Primjena nekih elementarnih funkcija u nizu Taylor i Maclorena .... 5 4. Primjena redova snage .... 7. SSED

Kvadratne jednadžbe Sadržaj Square Jednadžbe ... 4. I studija kvadratnih jednadžbi ... 4 .. Kvadratna jednadžba sa numeričkim koeficijentima ... 4 .. Riješite i istražite kvadratne jednake relativne

Odjeljak za zadatak s parametrima Komentari zadataka sa parametrima tradicionalno su složeni zadaci u strukturi upotrebe, koji zahtijevaju od podnositelja zahtjeva ne samo vlasništvo nad svim metodama i primanje rješenja za različite

Diferencijalni izračun uvod u matematičku analizu granica sekvence i funkcije. Otkrivanje nesigurnosti unutar. Izvedena funkcija. Pravila diferencijacije. DETIVAT ZA PRIJAVU

Fourierove serije ortogonalni sustavi funkcija sa stanovišta algebre ravnopravnosti gdje - funkcije ove klase A - koeficijenti iz R ili C jednostavno znači da je vektor linearne kombinacije vektora u

1. Određeni integral 1.1. Neka je F ograničena funkcija navedena u segmentu [, b] R. Podjela segmenta [, b] naziva se takav skup bodova τ \u003d (x, x 1, ..., XN 1, XN) [ , b], koji \u003d x< x 1 < < x n 1

Chulflage A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A A ujutro se zove serija više opći oblik: A A (a) (a) (a) (), gdje

treba:

1) Nacrtajte raspored f (x) na jaz u najmanje dva perioda za pokazivanje da je ova funkcija periodična;

2) Nacrtajte raspored S (x) Slično tome, da se vidi u kojim bodovima f (x) ¹s (x);

3) Izračunajte Fourierove koeficijente i napišite niz Fouriera.

Zadaci

№1. Furiate

Odluka. Primjetite, to f (x) postavljeno na dužini dužine T \u003d 4.. Jer f (x) Pretpostavlja se da je periodično, onda je taj broj njegov period, a zatim - l \u003d 2.

1) Grafikon f (x):

2) Grafikon S (x):

Strelice na krajevima linija pokazuju da funkcija ne prihvaća vrijednosti određene iz izraza navedenog u intervalu. Pri uspoređivanju grafova f (x) i S (x) To je jasno vidljivo da na pakiranju f (x) ¹s (x).

3) Izračunajte Fourier koeficijente. To se može učiniti formulama (3 *) :; ; . Upravo: ; Dakle,

Raspadanje f (x) Fourier ima obrazac:

Komentari. 1) kada se integrira na [-1;3] Ovaj segment je prekinut i jer Na tim segmentima f (x) Postavite različite vrijednosti.

2) Pri izračunavanju koeficijenata koji se koriste integrali: i, gde a \u003d Const.

№2 . Furiate

Odluka. Ovdje T \u003d 2., l \u003d 1..

Fourier serija ima obrazac: Gde; ; jer l \u003d 1..

1) Grafikon f (x):

2) Grafikon S (x):

№3. Raspadaju Fourieru na sinovima

Odluka. Imajte na umu da se samo neparne funkcije pokreću u Fourierovim sinusima. Jer f (x) Definisano samo za x\u003e 0, xî (0; 2) è (2; 3)onda to znači da je u simetričnom intervalu (-3; -2) è (-2; 0) f (x)treba nastaviti tako da jedna jednakost f (-x) \u003d -f (x). Stoga, dužina jaza na kojoj f (x) Postavljen je kao čudna funkcija, jednaka 6. Dakle T \u003d 6, l \u003d 3. Fourier serija za f (x) Ima obrazac:, gdje, n \u003d 1, 2, 3, (prema formulama (5 ")).

1) Grafikon f (x).

Za crtanje grafikona f (x) kao čudna funkcija, prvo nacrtajte raspored na (0; 2) è (2; 3), a zatim iskoristite činjenicu da je raspored čudne funkcije simetrično na početku koordinata. Iz tih razmatranja dobivamo raspored f (x) na (-3; -2) è (-2; 0). Zatim nastavite f (x) T \u003d 6..

2) Grafikon S (x).

Raspored S (x) Razlikuje se od rasporeda f (x) na brejku f (x). Na primjer, u t. x \u003d 2 f (x)nije definirano i S (x) ima u x \u003d 2. Što znači jednako polustrano ograničenje funkcija f (x), upravo: Gde ,.

Dakle, onda raspadanje f (x) Fourier ima obrazac :.

№4 . Otpremi Fourier na Cosineu.

Odluka. Imajte na umu da se samo čak i funkcije pokreću u nizu Fourieru na Cosineu. Jer f (x) Postavljeno samo za x\u003e 0, xî (0; 2) è (2; 3], onda to znači da je u simetričnom intervalu [-3; -2) è (-2; 0) f (x)potrebno je nastaviti tako da se izvrši jednakost: f (-x) \u003d f (x). Stoga, dužina jaza na kojoj f (x) Postavi kao ravnomjernu funkciju jednaka je 6, a zatim T \u003d 6, l \u003d 3. Fourier serija u ovom slučaju izgleda:

gde; ; n \u003d 1,2, ... (Prema formulama (4 ")).

1) Grafikon f (x).

Za crtanje grafikona f (x) kao čak funkcionira, prvo izvucite raspored f (x) na (0; 2) è (2; 3]A zatim iskoristite činjenicu da je grafikon ravnomjerne funkcije simetričan o osi ordinate. Iz tih razmatranja dobivamo raspored f (x) na [-3; -2) è (-2; 0). Zatim nastavite f (x) na cijeloj numeričkoj izrazi kao periodično funkcioniranje s periodom T \u003d 6..

Evo rasporeda f (x) Izvučeno u dva puna razdoblja funkcije.

2) Grafikon S (x).

Raspored S (x) Razlikuje se od rasporeda f (x) na brejku f (x). Na primjer, u t. x \u003d 0 f (x)nije definirano i S (x) Ima značenje: , pa raspored S (x) Nije prekinut u t. x \u003d 0., za razliku od rasporeda f (x).

Raspadanje f (x) U nizu Fourieru na Cosinesesu ima obrazac :.

№5. Furiate f (x) \u003d | x |, xî (-2; 2)..

Odluka. Uslovom, f (x) je čak funkcionalnost (-2;2) ; Oni. Njena Fourierova serija sadrži samo kosines, dok T \u003d 4, l \u003d 2, ,

gde; ; n \u003d 1, 2,

1) Grafikon f (x):

2) Grafikon S (x):

3), jer | X | \u003d X.za x\u003e 0.; .

Zatim propadaj f (x) Fourier ima obrazac :. Imajte na umu da prilikom integriranja izraza ili primjenjuje formulu integracije u dijelove: gdje u \u003d x; DV \u003d cos (Ax) DXili DV \u003d grijeh (AX) DX.

№6. Deparati funkciju u Fourierovoj seriji: a) u intervalu (-? ,?); b) u intervalu (0, 2?); c) u intervalu (0 ,?) u nizu sinusa.

Odluka. a) Funkcija grafikona sa 2? - Periodični nastavak je

Funkcija zadovoljava uvjete dirichlet teoreme i zato se može razgraditi u seriju Fouriera.

Izračunajte Fourierove koeficijente. Budući da je funkcija čak, tada BN \u003d 0 (n \u003d 0, 1, 2, ...) i (n \u003d 0, 1, 2, ...).

Za izračunavanje ovog integralnog, koristi se formula integracije u dijelove u određenom integralnom integralu. Primiti

Fourierov serija ove funkcije ima obrazac. Zbog znaka Dirichlea, ova serija predstavlja funkciju X2 u intervalu (-? ,?).

b) Interval (0, 2?) nije simetričan na početku koordinata, a njegova dužina 2 l. \u003d 2? Izračunajte Fourier koeficijente formulama:

Stoga Fourierie ima oblik. Na osnovu Dirichlet Theorem, serija se konvertira na generiranje funkcija na bodovima X? (0,2?), I na bodovima 0 i 2? smisao. Zbroj iznosa reda ima obrazac

c) Funkcija raspaljena u nizu sinusa treba biti neparna. Stoga ćemo navesti navedenu funkciju x2 u (-π, π) neparni način, I.E. Razmatramo funkciju. Za ovu funkciju F (x) imamo a \u003d 0 (n \u003d 0, 1, 2, ...) i

Željena raspadanje ima obrazac.

Zbroj iznosa reda ima obrazac

Imajte na umu da na bodovima x \u003d (-π, π), četveroierov red se konvergira na nulu.

№7 Položite funkciju navedenu grafički u Fourieru:

Odluka . Dobivamo eksplicitni izraz za f (x). Grafikon funkcije je ravna linija, koristimo jednadžbu direktno u obliku. Kao što se može vidjeti iz crteža ,, I.E. f (x) \u003d x - 1 (-1< x < 1) и период Т = 2.

Ova značajka zadovoljava uvjete dirichleta, pa se raspada u Fourierovu seriju. Izračunajte Fourierove koeficijente ( l. = 1):

; (n \u003d 1, 2, ...);

Fourier serija za funkciju f (x) ima pogled

Predstavlja funkciju F (x) na -1< x < 1, а в точках х0 = -1 и х0 = 1 ряд сходится к -1.

№8. Otpremajte funkciju u trigonometrijskom retku Fourieru na segmentu i navedite funkciju na koju se rezultirajuća serija konvergira.

Odluka.Nacrtajte raspored funkcije nastavkom povremeno s periodom ili na cijeloj osovini. Nastavak funkcija ima razdoblje.

Provjerite uvjete dovoljnih znakova konvergencije Fourierove serije (Dini-Lipschitsa, Jordan, Dirichlet).

Funkcija komadno monotona na segmentu: povećava se i dalje. Na bodovima funkcija ima prvu vrstu praznina.

Saznajte paritet ili neobičnost funkcije: funkcija nije ni ni ne čudna.

a) Ako je funkcija navedena na

b) Ako je funkcija postavljena na

Kreirajte FUNKCIJU TOFIER ROW :.

Navedite funkciju na koju će se ova serija konvergirati, koristeći trenutne znakove konvergencije: Prema znaku Dirichlea, Fourierov niz funkcija konvergira se na iznos:

№9. Eliminirajte funkciju u nizu Fourieru na sinovima na i uz pomoć ovog raspadanja da biste pronašli zbroj numeričke serije.

Odluka.Nastavite funkciju je čak (neparni) put (- p.0) ili (- - l.0), a zatim periodično sa periodom od 2 p. ili 2 l. Nastavite funkciju na cijeloj osovini.

Nastavljamo funkciju na neparan način, a zatim periodično, s periodom, nastavit ćemo ga cijeloj osovini.

Nacrtajte grafikon periodičnog nastavka. Dobit ćemo funkciju obrasca:

Provjerite uvjete dovoljnih znakova konvergencije Fourierove serije (Dini-Lipica, Jordan, Dirichlet).

Funkcija komadna konstantna u intervalu: jednak je -1 na i 1 na. Na bodovima funkcija ima prvu vrstu praznina.

Izračunajte Fourierove koeficijente:

Njeni četveroerični koeficijenti izračunavaju se formulama:

Napravite funkciju s redom Fourier. .

Navedite funkciju na koju će se ova serija konvergirati koristeći detektivske znakove konvergencije.

Prema znaku Dirichlea, brojne Fourierine funkcije se konvergira na iznos:

Slijedom toga, kao

Zamjena vrijednosti, odredite zbroj navedene numeričke serije.

Vjerujući u rezultirajuće raspadanje, naći ćemo

gde, jer.

№10. Napišite jednakost prioriteta za funkciju, a na osnovu ove jednakosti pronađite iznos numeričke serije.

Odluka.Instalirajte da li je ova funkcija funkcija s integriranim kvadratom.

Funkcija je kontinuirana, a samim tim i integrirana. Iz istog razloga, njegov se kvadrat integrira.

Izračunajte Fourier koeficijente formulama:

Od neparnog funkcije, tada su njeni Fourierovi koeficijenti izračunavaju formulama:

Izračunati integralni.

Napišite parseval formule:

Dakle, Formula Parseval ima obrazac

Ugovoreno, ako je potrebno, aritmetičke akcije u desnim i lijevim dijelovima, kako bi se dobila iznos ove numeričke serije.

Dijeljenje oba dijela jednakosti dobivene sa 144, nalazimo:.

№11. Pronađite Fourierove integrirane funkcije

i izgradite raspored.

Odluka.Izgradite grafikon funkcije.

Provjerite ispunjavanje uvjeta dovoljnih znakova konvergencije Fourierovog integralnog (Dini, Dirichlet-jordan ili posljedice).

Funkcija je apsolutno integrirana u jaz, kontinuirano kada i, a u trenutku postoji jaz prve vrste. Nadalje, sa i funkcija ima konačnu derivaciju, a finalni desni i lijevi derivati \u200b\u200bpostoje u nuli. Saznajte paritet ili neobičnost funkcije. Funkcija nije ni ni ni čudna. ; .

Dakle, ili,

U blizini Fourierova Funkcije F (x) u intervalu (-π; π) nazivaju se trigonometrijskim serijama obrasca:
gde

Blizu Fourierove funkcije f (x) u intervalu (-L; l) naziva se trigonometrijska serija obrasca:
gde

Svrha. Online kalkulator Dizajniran za razgradnju funkcije f (x) u nizu Fourieru.

Za funkcije modula (na primjer, | x |), koristiti dekompozicija kozinom.

Pravila za unos funkcija:

Za funkcije modula koristite kosinus raspadanje. Na primjer, za X | Potrebno je unijeti funkciju bez modula, I.E. x.

Čečno serije Fourierove serije neprekidno, komadno monotono i ograničeno na intervalu (- l.;l.) Funkcije se konvergiraju na cijeloj numeričkoj osi.

Zbroj Fourierovog serije S (x):

• to je periodična funkcija sa periodom od 2 l.. Funkcija U (x) naziva se periodična s periodom T (ili T-periodična), ako za sve X regije r, u (x + t) \u003d u (x).
• u intervalu (- l.;l.) poklapa se sa funkcijom f.(x.), osim za lomljenje bodova
• na Break bodovima (prva vrsta, jer funkcija je ograničena) funkcije f.(x.) I na krajevima intervala traje prosjeci:

.
Kaže se da je funkcija postavljena u Fourierovoj seriji u intervalu (- l.;l.): .

Ako a f.(x.) - Čak i funkcija, tada su samo čak i funkcije uključene u njegovu raspadanje, odnosno, b N.=0.
Ako a f.(x.) - čudna funkcija, tada su samo neparne funkcije uključene u njenu raspadanje, odnosno, a N.=0

U blizini Fourierova Funkcije f.(x.) u intervalu (0; l.) na Cosine Dougses Pozvani red:
gde
.
U blizini Fourierova Funkcije f.(x.) u intervalu (0; l.) na sinovima višestrukih luka Pozvani red:
gde .
Zbroj serije Fouriera kosinu višestrukih lukova je još periodična funkcija sa razdobljem od 2 l.Poklapa S. f.(x.) u intervalu (0; l.) Na tačkice kontinuiteta.
Zbroj serije Fourierove u sinovima višestrukih lukova neobična je periodična funkcija sa razdobljem od 2 l.Poklapa S. f.(x.) u intervalu (0; l.) Na tačkice kontinuiteta.
Fourier serija za ovu funkciju u ovom intervalu ima svojstvo jedinstvenosti, odnosno ako se raspadanje dobiva na bilo koji drugi način od upotrebe formula, na primjer, koristeći selekciju koeficijenata, tada se ovi koeficijenti podudaraju s formulama izračunatim formule.

Primjer broj 1. Položite funkciju f (x) \u003d 1:
a) U punom rasponu Fourieru u intervalu(-π ;π);
b) zaredom na sinovima višestrukih lukova u intervalu(0;π); izgradite grafikon rezultirajuće Fourier serije
Odluka:
a) raspadanje u Fourierovoj seriji u intervalu (-π; π) ima obrazac:
,
i svi koeficijenti b N.\u003d 0, jer Ova značajka je čak; na ovaj način,

Očito će se jednakost izvoditi ako uzmete
ali 0 =2, ali 1 =ali 2 =ali 3 =…=0
Na osnovu svojstava jedinstvenosti, ovo su željeni koeficijenti. Dakle, željena raspadanja: ili samo 1 \u003d 1.
U ovom slučaju, kada serija identično podudara sa svojom funkcijom, raspored serije Fourieru poklapa se s rasporedom funkcije na cijeloj numeričkoj liniji.
b) Dekompozicija u intervalu (0; π) na sinovima višestrukih lukova ima oblik:
Nemoguće je odabrati koeficijente tako da je jednakost identično nemoguće. Koristimo formulu za izračunavanje koeficijenata:


Dakle, za čak n. (n.=2k.) Imati b N.\u003d 0, za neparno ( n.=2k.-1) -
Napokon, .
Izgrađujemo grafikon rezultirajuće Fourier serije koristeći njegove svojstva (vidi gore).
Prije svega, izgrađujemo grafikon ove funkcije u određenom intervalu. Zatim, koristeći tačnost zbroja broja, nastavljamo raspored simetrično početkom koordinata:

Nastavljamo na periodičan način na cijeloj numeričkoj osi:


I na kraju, na javnim bodovima ispunite prosjek (između desne i lijeve granice) vrijednosti:

Primjer broj 2. Odbaci funkciju U intervalu (0; 6) na sinovima višestrukih lukova.
Odluka: Željeni raspadanje ima obrazac:

Od leve strane, a pravi deo ravnopravnosti sadrži samo funkcije Grijeh. Iz različitih argumenata provjerite da li odgovaraju bilo kakvim vrijednostima n (prirodnih!) Argumenti sinusa u lijevom i desnom dijelu ravnopravnosti:
Ili, odakle n \u003d 18. To znači da se takav pojam nalazi na desnoj strani, a koeficijent s tim mora se podudarati s koeficijentom na lijevoj strani: b. 18 =1;
Ili, odakle n \u003d 4. To znači b. 4 =-5.
Dakle, uz pomoć odabira koeficijenata moguće je dobiti željenu raspadanje.