Знаходження коефіцієнтів ряду Фур'є. Визначення коефіцієнтів ряду за формулами фурье
Ряд Фур'є періодичних функцій з періодом 2π.
Ряд Фур'є дозволяє вивчати періодичні функції, розкладаючи їх на компоненти. Змінні струми і напруги, зміщення, швидкість і прискорення кривошипно-шатунних механізмів і акустичні хвилі - це типові практичні приклади застосування періодичних функцій в інженерних розрахунках.
Розкладання в ряд Фур'є грунтується на припущенні, що всі, хто має практичне значення функції в інтервалі -π ≤x≤ π можна виразити у вигляді сходяться тригонометричних рядів (ряд вважається сходящимся, якщо сходиться послідовність часткових сум, складених з його членів):
Стандартна (\u003d звичайна) запис через суму sinx і cosx
f (x) \u003d a o + a 1 cosx + a 2 cos2x + a 3 cos3x + ... + b 1 sinx + b 2 sin2x + b 3 sin3x + ...,
де a o, a 1, a 2, ..., b 1, b 2, .. - дійсні константи, тобто
Де для діапазону від -π до π коефіцієнти ряду Фур'є розраховуються за формулами:

Коефіцієнти a o, a n і b n називаються коефіцієнтами Фур'є, І якщо їх можна знайти, то ряд (1) називається поруч Фур'є, відповідним функції f (x). Для ряду (1) член (a 1 cosx + b 1 sinx) називається першою або основною гармонікою,
Інший спосіб запису ряду - використання співвідношення acosx + bsinx \u003d csin (x + α)
f (x) \u003d a o + c 1 sin (x + α 1) + c 2 sin (2x + α 2) + ... + c n sin (nx + α n)
Де a o - константа, з 1 \u003d (a 1 2 + b 1 2) 1/2, з n \u003d (a n 2 + b n 2) 1/2 - амплітуди різних компонент, а дорівнює a n \u003d arctg a n / b n.
Для ряду (1) член (a 1 cosx + b 1 sinx) або c 1 sin (x + α 1) називається першою або основною гармонікою, (A 2 cos2x + b 2 sin2x) або c 2 sin (2x + α 2) називається другий гармонікою і так далі.
Для точного уявлення складного сигналу зазвичай потрібно нескінченну кількість членів. Однак у багатьох практичних завданнях досить розглянути тільки кілька перших членів.
Ряд Фур'є неперіодичних функцій з періодом 2π.
Розкладання неперіодичних функцій.
Якщо функція f (x) неперіодичних, значить, вона не може бути розкладена в ряд Фур'є для всіх значень х. Однак можна визначити ряд Фур'є, який представляє функцію в будь-якому діапазоні шириною 2π.
Якщо задана неперіодичних функція, можна скласти нову функцію, вибираючи значення f (x) в певному діапазоні і повторюючи їх поза цього діапазону з інтервалом 2π. Оскільки нова функція є періодичною з періодом 2π, її можна розкласти в ряд Фур'є для всіх значень х. Наприклад, функція f (x) \u003d x не є періодичною. Однак, якщо необхідно розкласти її в ряд Фур'є на інтервалі від про до 2π, тоді поза цим інтервалом будується періодична функція з періодом 2π (як показано на рис. Нижче).

Для неперіодичних функцій, таких як f (x) \u003d х, сума ряду Фур'є дорівнює значенню f (x) у всіх точках заданого діапазону, але вона не дорівнює f (x) для точок поза діапазону. Для знаходження ряду Фур'є неперіодичної функції в діапазоні 2π використовується все таже формула коефіцієнтів Фур'є.
Парні і непарні функції.
Кажуть, функція y \u003d f (x) парна, Якщо f (-x) \u003d f (x) для всіх значень х. Графіки парних функцій завжди симетричні щодо осі у (тобто є дзеркально відображеними). Два приклади парних функцій: у \u003d х 2 і у \u003d cosx.
Кажуть, що функція y \u003d f (x) непарна,якщо f (-x) \u003d - f (x) для всіх значень х. Графіки непарних функцій завжди симетричні відносно початку координат.
Багато функцій не є ні парними, ні непарними.
Розкладання в ряд Фур'є по косинусам.
Ряд Фур'є парної періодичної функції f (x) з періодом 2π містить тільки члени з косинусами (тобто не містить членів з синусами) і може включати постійний член. отже,

де коефіцієнти ряду Фур'є,

Ряд Фур'є непарної періодичної функції f (x) з періодом 2π містить тільки члени з синусами (тобто не містить членів з косинусами).
отже,

де коефіцієнти ряду Фур'є,
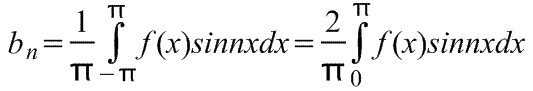
Ряд Фур'є на напівперіоді.
Якщо функція визначена для діапазону, скажімо від 0 до π, а не тільки від 0 до 2π, її можна розкласти в ряд тільки по синусах або тольо по косинусам. Отриманий ряд Фур'є називається поруч Фур'є на напівперіоді.
Якщо потрібно отримати розкладання Фур'є на напівперіоді по косинусамфункції f (x) в діапазоні від 0 до π, то необхідно скласти парну періодичну функцію. На рис. нижче показана функція f (x) \u003d х, побудована на інтервалі від х \u003d 0 до х \u003d π. Оскільки парна функція симетрична щодо осі f (x), проводимо лінію АВ, як показано на рис. нижче. Якщо припустити, що за межами розглянутого інтервалу отримана трикутна форма є періодичною з періодом 2π, то підсумковий графік має вигляд, показ. на рис. нижче. Оскільки потрібно отримати розкладання Фур'є по косинусам, як і раніше, обчислюємо коефіцієнти Фур'є a o і a n


Якщо потрібно отримати розкладання Фур'є на напівперіоді по синусах функції f (x) в діапазоні від 0 до π, то необхідно скласти непарну періодичну функцію. На рис. нижче показана функція f (x) \u003d x, побудована на інтервалі від від х \u003d 0 до х \u003d π. Оскільки непарна функція симетрична щодо початку координат, будуємо лінію CD, як показано на рис. Якщо припустити, що за межами розглянутого інтервалу отриманий пилкоподібний сигнал є періодичним з періодом 2π, то підсумковий графік має вигляд, показаний на рис. Оскільки потрібно отримати розкладання Фуріе на напівперіоді по синусах, як і раніше, обчислюємо коефіцієнт Фур'є. b

Ряд Фур'є для довільного інтервалу.
Розкладання періодичної функції з періодом L.
Періодична функція f (x) повторюється при збільшенні х на L, тобто f (x + L) \u003d f (x). Перехід від розглянутих раніше функцій з періодом 2π до функцій з періодом L досить простий, оскільки його можна здійснити за допомогою заміни змінної.
Щоб знайти ряд Фур'є функції f (x) в діапазоні -L / 2≤x≤L / 2, введемо нову змінну u таким чином, щоб функція f (x) мала період 2π щодо u. Якщо u \u003d 2πх / L, то х \u003d -L / 2 при u \u003d -π і х \u003d L / 2 при u \u003d π. Також нехай f (x) \u003d f (Lu / 2π) \u003d F (u). Ряд Фур'є F (u) має вигляд
(Межі інтегрування можуть бути замінені на будь-який інтервал довжиною L, наприклад, від 0 до L)
Ряд Фур'є на напівперіоді для функцій, заданих в інтервалі L ≠ 2π.
Для підстановки u \u003d πх / L інтервал від х \u003d 0 до х \u003d L відповідає інтервалу від u \u003d 0 до u \u003d π. Отже, функцію можна розкласти в ряд тільки по косинусам або тільки по синусах, тобто в ряд Фур'є на напівперіоді.
Розкладання по косинусам в діапазоні від 0 до L має вигляд

Одним з видів функціональних рядів є тригонометричний ряд
Ставиться завдання підібрати коефіцієнти ряду так, щоб він сходився до заданої в інтервалі [-π, π] функції; інакше кажучи, потрібно розкласти цю функцію в тригонометричний ряд. Достатня умова розв'язання цього завдання полягає в тому, щоб функція була в інтервалі [-π, π] кусочно-безперервна і кусочно-дифференцируема, т. Е. Щоб інтервал [-π, π] міг бути розбитий на кінцеве число часткових інтервалів, в кожному з яких дана функція неперервна і має похідну (на кінцях часткових інтервалів функція повинна мати кінцеві односторонні межі і односторонні похідні, при обчисленні яких в якості значення функції в кінці часткового інтервалу береться її односторонній межа). Умова кусочной дифференцируемости може бути замінено умовою кусочной монотонності функції, т. Е. Вимогою, щоб в кожному з часткових інтервалів функція була монотонна. Достатньою умовою разложимости функції в інтервалі [-π, π] в тригонометричний ряд є також вимога, щоб в цьому інтервалі функція мала обмежену зміну. За визначенням функції f (x) має в інтервалі обмежену зміну, якщо при будь-якому розбитті цього інтервалу на кінцеве число інтервалів
величина
обмежена зверху одним і тим же числом.
Саме з такими функціями доводиться мати справу при вирішенні практичних завдань.
При виконанні будь-якого з трьох зазначених достатніх умов функція f (x) представляється в інтервалі [-π, π] тригонометричним рядом, у якого коефіцієнти визначаються за формулами
При таких коефіцієнтах тригонометричний ряд називається поруч Фур'є. Цей ряд сходиться до f (x) в кожній точці її безперервності; в точках розриву він сходиться до середнього арифметичного лівого і правого граничних значень, т. е. k, якщо х є точка розриву (рис. 1); на кордонах відрізка ряд сходиться к.
Малюнок 1.
Функція, що виражається поруч Фур'є, є функція періодична, а тому ряд, складений для функції, заданої на відрізку [-π, π], сходиться поза цим відрізком до періодичному продовження цієї функції (рис. 2).
Малюнок 2.
Якщо поруч Фур'є представляється функція f (x), задана в довільному інтервалі [α, α + 2π] довжиною 2π, то коефіцієнти ряду а 0, ak, bk (коефіцієнти Фур'є) можна визначити за вказаними формулами, в яких межі інтегрування замінені на α і α + 2π. Взагалі, оскільки в формулах для а 0, a k, b до стоять функції з періодом 2π, інтегрування можна проводити з будь-якого інтервалу з довжиною 2π.
Ряд Фур'є може бути використаний для наближеного представлення функції, а саме: функція f (x) замінюється приблизно рівною їй сумою s n (x) перших кількох членів ряду Фур'є:
Вираз sn (x), де а 0, ak, bk є коефіцієнтами Фур'є функції f (x), у порівнянні з іншими виразами такого ж виду з тим же значенням n, але з іншими коефіцієнтами, призводить до мінімального середньому квадратичному відхиленню sn (x ) від f (х), яке визначається як
Залежно від роду симетрії функції можливі деякі спрощення. Якщо функція парна, т. Е. F (-x) \u003d f (x), то
і функція розкладається в ряд по косинусам. Якщо функція непарна, т. Е. F (-х) \u003d - f (x), то
і функція розкладається в ряд по синусах. Якщо функція задовольняє умові f (x + π) \u003d - f (x), т. Е. Крива, що відноситься до половині відрізка довжиною 2π, є дзеркальним відображенням іншої половини кривої, то
Функція може бути задана не тільки на відрізку довжиною 2π, але також на відрізку будь-якої довжини 2l. Якщо вона на цьому відрізку задовольняє наведеним вище умовам, то вона разложима в ряд Фур'є такого вигляду:
причому коефіцієнти ряду обчислюються за формулами
У табл. 1 дані розкладання деяких функцій.
Таблиця 1.
Тригонометричний ряд можна записати і в такому вигляді:
Ряд Фур'є функції f (x) сходиться тим швидше, чим більш гладкою є функція. Якщо функція f (x) і її похідні f "(x), f" (x), ..., fk -1 (x) всюди неперервні, а f (k) (x) допускає лише точки розриву 1-го роду в кінцевому числі, то коефіцієнти Фур'є а n, bn функції f (х) будуть
Символом позначається така величина, що
Розкладання в тригонометричний ряд називають гармонійним аналізом, а тригонометричні функції, Що входять в цей ряд, - гармоніками. Обчислення за складовими гармоникам називається гармонійним синтезом.
При розрахунках конструкцій часто доводиться розкладати в ряд Фур'є різні функції, Задані графіками, і перш за все зображують навантаження. У табл. 2 і 3 дані розкладання для деяких функцій, характерних для навантажень, в тому числі і ряди, відповідні зосередженим силам.
Таблиця 2.
Графік функцій |
ряд Фур'є |
n |
транскрипт
1 МІНІСТЕРСТВО ОСВІТИ І НАУКИ РФ Новосибірський державний університет ФІЗИЧНИЙ ФАКУЛЬТЕТ Р. К. Бельхеева ЛАВИ ФУР'Е В ПРИКЛАДАХ І ЗАВДАННЯ Навчальний посібник Новосибірськ 211
2 УДК ББК В161 Б44 Б44 Бельхеева Р. К. Ряди Фур'є в прикладах і завданнях: Навчальний посібник / Новосиб. держ. ун-т. Новосибірськ, с. ISBN У навчальному посібнику викладаються основні відомості про рядах Фур'є, наведені приклади на кожну досліджувану тему. Детально розібрано приклад застосування методу Фур'є до розв'язання задачі про поперечні коливання струни. Наведено ілюстративний матеріал. Є завдання для самостійного рішення. Призначено для студентів і викладачів фізичного факультету НГУ. Друкується за рішенням методичної комісії фізичного факультету НГУ. Рецензент д-р фіз.-мат. наук. В. А. Александров Посібник підготовлено в рамках реалізації Програми розвитку НДУ-НГУ на рр. ISBN c Новосибірський державний університет, 211 c Бельхеева Р. К., 211
3 1. Розпад 2π-періодичної функції в ряд Фур'є Визначення. Поруч Фур'є функції f (x) називається функціональний ряд a 2 + (an cosnx + bn sin nx), (1) де коефіцієнти an, bn обчислюються за формулами: an \u003d 1 π bn \u003d 1 π f (x) cosnxdx, n \u003d , 1, ..., (2) f (x) sin nxdx, n \u003d 1, 2, .... (3) Формули (2) (3) називають формулами Ейлера Фур'є. Той факт, що функції f (x) відповідає ряд Фур'є (1) записують у вигляді формули f (x) a 2 + (an cosnx + bn sin nx) (4) і говорять, що права частина формули (4) є формальним поруч Фур'є функції f (x). Іншими словами, формула (4) означає тільки те, що коефіцієнти a n, b n знайдені за формулами (2), (3). 3
4 Визначення. 2π-періодична функція f (x) називається кусочно-гладкою, якщо в проміжку [, π] знайдеться кінцеве число точок \u003d x< x 1 <... < x n = π таких, что в каждом открытом промежутке (x j, x j+1) функция f(x) непрерывно дифференцируема, а в каждой точке x j существуют конечные пределы слева и справа: f(x j) = lim h + f(x j h), f(x j +) = lim h + f(x j + h), (5) f(x j h) f(x j) f(x j + h) f(x j +) lim, lim. h + h h + h (6) Отметим, что последние два предела превратятся в односторонние производные после замены предельных значений f(x j) и f(x j +) значениями f(x j). Теорема о представимости кусочно-гладкой функции в точке своим рядом Фурье (теорема о поточечной сходимости). Ряд Фурье кусочно-гладкой 2π-периодической функции f(x) сходится в каждой точке x R, а его сумма равна числу f(x), если x точка непрерывности функции f(x), f(x +) + f(x) и равна числу, если x точка разрыва 2 функции f(x). ПРИМЕР 1. Нарисуем график, найдем ряд Фурье функции, заданной на промежутке [, π] формулой, f(x) = x, предполагая, что она имеет период 2π, и вычислим суммы 1 1 числовых рядов (2n + 1) 2, n 2. n= Решение. Построим график функции f(x). Получим кусочно-линейную непрерывную кривую с изломами в точках x = πk, k целое число (рис. 1). 4
5 Рис. 1. Графік функції f (x) Обчислимо коефіцієнти Фур'є a \u003d 1 π f (x) dx \u003d 1 π x 2 2 π \u003d π, an \u003d 1 π f (x) cosnxdx \u003d 2 π \u003d 2 () x sin nx cos nx + π nn 2 \u003d 2 π (1) n 1 n 2 \u003d bn \u003d 1 π π \u003d 2 π f (x) cosnxdx \u003d cos nx cos n 2 \u003d 4 πn2, при n непарному, при n парному, f (x ) sin nxdx \u003d, тому що функція f (x) парна. Запишемо формальний ряд Фур'є для функції f (x): f (x) π 2 4 π k \u003d 5 cos (2k + 1) x (2k + 1) 2.
6 З'ясуємо чи є функція f (x) кусочно-гладкою. Так як вона неперервна, обчислимо тільки межі (6) в кінцевих точках проміжку x \u003d ± π і в точці зламу x \u003d: і f (π h) f (π) π h π lim \u003d lim h + hh + h \u003d 1, f (+ h) f (+) + h () lim \u003d lim h + hh + hf (+ h) f (+) + h lim \u003d lim \u003d 1, h + hh + h \u003d 1, f (h) f () h () lim \u003d lim \u003d 1. h + hh + h Межі існують і кінцеві, отже, функція кусочно-гладка. По теоремі про поточечной збіжності її ряд Фур'є сходиться до числа f (x) в кожній точці, т. Е. F (x) \u003d π 2 4 π k \u003d cos (2k + 1) + x (2k + 1) 2 \u003d \u003d π 2 4 (cosx + 19 π cos 3x) cos 5x (7) На рис. 2, 3 показаний характер наближення часткових сум ряду Фур'є S n (x), де S n (x) \u003d an 2 + (ak coskx + bk sin kx), k \u003d 1 до функції f (x) в проміжку [, π] . 6
7 Рис. 2. Графік функції f (x) з накладеними на нього графіками часткових сум S (x) \u003d a 2 і S 1 (x) \u003d a 2 + a 1 cos x Рис. 3. Графік функції f (x) з накладеним на нього графіком часткової суми S 99 (x) \u003d a 2 + a 1 cos x + + a 99 cos 99x 7
8 Підставивши в (7) x \u003d отримаємо: \u003d π 2 4 π k \u003d 1 (2k + 1) 2, звідки ми знаходимо суму числового ряду: \u003d π2 8. Знаючи суму цього ряду, легко знайти наступну суму Маємо: S \u003d ( ) S \u003d () \u003d π S, отже S \u003d π2 6, тобто 1 n \u003d π Суму цього знаменитого ряду вперше знайшов Леонард Ейлер. Вона часто зустрічається в математичному аналізі і його додатках. ПРИКЛАД 2. Намалюємо графік, знайдемо ряд Фур'є функції заданої формулою f (x) \u003d x для x< π, предполагая, что она имеет период 2π, и вычислим суммы числовых (1) n) рядов + n= ((2n + 1,) (k k + 1) Решение. График функции f(x) приведен на рис. 4. 8
9 Рис. 4. Графік функції f (x) Функція f (x) неперервно-диференційована на проміжку (, π). У точках x \u003d ± π, вона має кінцеві межі (5): f () \u003d, f (π) \u003d π. Крім того існують кінцеві межі (6): f (+ h) f (+) lim \u003d 1 і h + hf (π h) f (π +) lim \u003d 1. h + h Значить, f (x) кусочно-гладка функція. Так як функція f (x) непарна, то a n \u003d. Коефіцієнти bn знаходимо інтегруванням частинами: bn \u003d 1 π f (x) sin πnxdx \u003d 1 [x cosnx π πn + 1 n \u003d 1 πn [(1) n π + (1) n π] \u003d 2 (1) n + 1. n Складемо формальний ряд Фур'є функції 2 (1) n + 1 f (x) sin nx. n 9 cosnxdx] \u003d
10 Згідно з теоремою про поточечной збіжності кусочно-гладкою 2π-періодичної функції ряд Фур'є функції f (x) сходиться до суми: 2 (1) n + 1 sin nx \u003d n f (x) \u003d x, якщо π< x < π, = f(π) + f(π +) 2 =, если x = π, (8) f() + f(+) =, если x =. 2 На рис. 5 8 показан характер приближения частичных сумм S n (x) ряда Фурье к функции f(x). Рис. 5. График функции f(x) с наложенным на него графиком частичной суммы S 1 (x) = a 2 + a 1 cos x 1
11 Рис. 6. Графік функції f (x) з накладеним на нього графіком часткової суми S 2 (x) Рис. 7. Графік функції f (x) з накладеним на нього графіком часткової суми S 3 (x) 11
12 Рис. 8. Графік функції f (x) з накладеним на нього графіком часткової суми S 99 (x) Використовуємо отриманий ряд Фур'є для знаходження сум двох числових рядів. Покладемо в (8) x \u003d π / 2. Тоді 2 () + ... \u003d π 2, або \u003d n \u003d (1) n 2n + 1 \u003d π 4. Ми легко знайшли суму відомого ряду Лейбніца. Поклавши в (8) x \u003d π / 3, знайдемо () + ... \u003d π 2, 3, або (1 + 1) () (k) 3π + ... \u003d 3k
13 ПРИКЛАД 3. Намалюємо графік, знайдемо ряд Фур'є функції f (x) \u003d sin x, припускаючи, що вона має період 2π, і 1 обчислимо суму числового ряду 4n 2 1. Рішення. Графік функції f (x) наведено на рис. 9. Очевидно, f (x) \u003d sin x безперервна парна функція з періодом π. Але 2π теж є періодом функції f (x). Мал. 9. Графік функції f (x) Обчислимо коефіцієнти Фур'є. Всі b n \u003d тому, що функція парна. Користуючись тригонометричними формулами обчислимо an при n 1: an \u003d 1 π \u003d 1 π sin x cosnxdx \u003d 2 π sin x cosnxdx \u003d (sin (1 + n) x sin (1 n) x) dx \u003d \u003d 1 () π cos ( 1 + n) x cos (1 n) x + \u003d 2 () 1 + (1) n \u003d π 1 + n 1 n π 1 n 2 (4 1, якщо n \u003d 2k, \u003d π n 2 1, якщо n \u003d 2k
14 Це обчислення не дозволяє нам знайти коефіцієнт a 1, тому що при n \u003d 1 знаменник звертається в нуль. Тому обчислимо коефіцієнт a 1 безпосередньо: a 1 \u003d 1 π sin x cosxdx \u003d. Так як f (x) неперервно диференційовна на (,) і (, π) і в точках kπ, (k ціле число), існують кінцеві межі (5) і (6), то ряд Фур'є функції сходиться до неї в кожній точці: \u003d 2 π 4 π sinx \u003d 2 π 4 π cos 2nx 4n 2 1 \u003d (1 1 cos 2x cos 4x + 1) cos 6x На рис показаний характер наближення функції f (x) частковими сумами ряду Фур'є .. (9) рис. 1. Графік функції f (x) з накладеним на нього графіком часткової суми S (x) 14
15 Рис. 11. Графік функції f (x) з накладеним на нього графіком часткової суми S 1 (x) Рис. 12. Графік функції f (x) з накладеним на нього графіком часткової суми S 2 (x) Рис. 13. Графік функції f (x) з накладеним на нього графіком часткової суми S 99 (x) 15
16 1 Обчислимо суму числового ряду. Для цього 4n 2 1 покладемо в (9) x \u003d. Тоді cosnx \u003d 1 для всіх n \u003d 1, 2, ... і Отже, 2 π 4 π 1 4n 2 1 \u003d. 1 4n 2 1 \u003d \u003d 1 2. ПРИКЛАД 4. Доведемо, що якщо кусково-гладка безперервна функція f (x) задовольняє умові f (x π) \u003d f (x) для всіх x (т. Е. Є π-періодичної) , то a 2n 1 \u003d b 2n 1 \u003d для всіх n 1, і навпаки, якщо a 2n 1 \u003d b 2n 1 \u003d для всіх n 1, то f (x) π-періодична. Рішення. Нехай функція f (x) є π-періодичної. Обчислимо її коефіцієнти Фур'є a 2n 1 і b 2n 1: \u003d 1 π (a 2n 1 \u003d 1 π f (x) cos (2n 1) xdx + f (x) cos (2n 1) xdx \u003d) f (x) cos (2n 1) xdx. У першому інтегралі зробимо заміну змінної x \u003d t π: f (x) cos (2n 1) xdx \u003d f (t π) cos (2n 1) (t + π) dt. 16
17 Користуючись тим, що cos (2n 1) (t + π) \u003d cos (2n 1) t і f (t π) \u003d f (t), отримаємо: a 2n 1 \u003d 1 π (f (x) cos (2n 1) x dx +) f (x) cos (2n 1) x dx \u003d. Аналогічно доводиться, що b 2n 1 \u003d. Навпаки, нехай a 2n 1 \u003d b 2n 1 \u003d. Так як функція f (x) неперервна, то по теоремі про представимости функції в точці своїм поруч Фур'є маємо Тоді f (x π) \u003d \u003d f (x) \u003d (a 2n cos 2nx + b 2n sin 2nx). (A2n cos 2n (x π) + b 2n sin 2n (x π)) \u003d (a2n cos 2nx + b 2n sin 2nx) \u003d f (x), що і означає, що f (x) є π-періодичною функцією. ПРИКЛАД 5. Доведемо, що якщо кусково-гладка функція f (x) задовольняє умові f (x) \u003d f (x) для всіх x, то a \u003d і a 2n \u003d b 2n \u003d для всіх n 1, і навпаки, якщо a \u003d a 2n \u003d b 2n \u003d, то f (x π) \u003d f (x) для всіх x. Рішення. Нехай функція f (x) задовольняє умові f (x π) \u003d f (x). Обчислимо її коефіцієнти Фур'є: 17
18 \u003d 1 π (a n \u003d 1 π f (x) cos nxdx + f (x) cosnxdx \u003d) f (x) cosnxdx. У першому інтегралі зробимо заміну змінної x \u003d t π. Тоді f (x) cosnxdx \u003d f (t π) cosn (t π) dt. Користуючись тим, що cos n (t π) \u003d (1) n cosnt і f (t π) \u003d f (t), отримаємо: an \u003d 1 π ((1) n) f (t) cosnt dt \u003d, якщо n парне, \u003d 2 π f (t) cos nt dt, якщо n непарне. π Аналогічно доводиться, що b 2n \u003d. Навпаки, нехай a \u003d a 2n \u003d b 2n \u003d, для всіх n 1. Так як функція f (x) неперервна, то по теоремі про представимости функція в точці своїм поруч Фур'є справедливо рівність f (x) \u003d (a 2n 1 cos ( 2n 1) x + b 2n 1 sin (2n 1) x). 18
19 Тоді \u003d f (x π) \u003d \u003d \u003d f (x). ПРИКЛАД 6. Вивчимо як слід продовжити інтегруються на проміжку [, π / 2] функцію f (x) на проміжок [, π], щоб її ряд Фур'є мав вигляд: a 2n 1 cos (2n 1) x. (1) Рішення. Нехай графік функції має вигляд, наведений на рис. 14. Оскільки в ряді (1) a \u003d a 2n \u003d b 2n \u003d для всіх n, то з прикладу 5 випливає, що функція f (x) повинна задовольняти рівності f (x π) \u003d f (x) для всіх x. Це спостереження дає спосіб продовження функції f (x) на проміжок [, / 2]: f (x) \u003d f (x + π), рис. 15. З того, що ряд (1) містить тільки косинуси, робимо висновок, що продовжена функція f (x) повинна бути парному (т. Е. Її графік повинен бути симетричний щодо осі Oy), рис
20 Рис. 14. Графік функції f (x) Рис. 15. Графік продовження функції f (x) на проміжок [, / 2] 2
21 Отже, шукана функція має вигляд, наведений на рис. 16. Рис. 16. Графік продовження функції f (x) на проміжок [, π] Підводячи підсумок, робимо висновок що функцію слід продовжити в такий спосіб: f (x) \u003d f (x), f (π x) \u003d f (x), тобто на проміжку [π / 2, π], графік функції f (x) центрально симетричний відносно точки (π / 2,), а на проміжку [, π] її графік симетричний відносно осі Oy. 21
22 УЗАГАЛЬНЕННЯ ПРИКЛАДІВ 3 6 Нехай l\u003e. Розглянемо дві умови: а) f (l x) \u003d f (x); б) f (l + x) \u003d f (x), x [, l / 2]. З геометричної точки зору умова (а) означає, що графік функції f (x) симетричний відносно вертикальної прямої x \u003d l / 2, а умова (б) що графік f (x) центрально симетричний відносно точки (l / 2;) на осі абсцис. Тоді справедливі наступні твердження: 1) якщо функція f (x) парна і виконана умова (а), то b 1 \u003d b 2 \u003d b 3 \u003d ... \u003d, a 1 \u003d a 3 \u003d a 5 \u003d ... \u003d; 2) якщо функція f (x) парна і виконана умова (б), то b 1 \u003d b 2 \u003d b 3 \u003d ... \u003d, a \u003d a 2 \u003d a 4 \u003d ... \u003d; 3) якщо функція f (x) непарна і виконана умова (а), то a \u003d a 1 \u003d a 2 \u003d ... \u003d, b 2 \u003d b 4 \u003d b 6 \u003d ... \u003d; 4) якщо функція f (x) непарна і виконана умова (б), то a \u003d a 1 \u003d a 2 \u003d ... \u003d, b 1 \u003d b 3 \u003d b 5 \u003d ... \u003d. ЗАВДАННЯ В задачах 1 7 намалюйте графіки і знайдіть ряди Фур'є для функцій, (припускаючи, що вони мають період 2π :, якщо< x <, 1. f(x) = 1, если < x < π. 1, если < x < /2, 2. f(x) =, если /2 < x < π/2, 1, если π/2 < x < π. 3. f(x) = x 2 (< x < π). 4. f(x) = x 3 (< x < π). { π/2 + x, если < x <, 5. f(x) = π/2 x, если < x < π. 22
23 (1, якщо / 2< x < π/2, 6. f(x) = 1, если π/2 < x < 3π/2. {, если < x <, 7. f(x) = sin x, если < x < π. 8. Как следует продолжить интегрируемую на промежутке [, π/2] функцию f(x) на промежуток [, π], чтобы ее ряд Фурье имел вид: b 2n 1 sin (2n 1)x? Ответы sin(2n 1)x sin(2n + 1)x. π 2n 1 π 2n + 1 n= 3. 1 (1) n () 12 3 π2 + 4 cosnx. 4. (1) n n 2 n 2π2 sin nx. 3 n 5. 4 cos(2n + 1)x π (2n + 1) (1) n cos(2n + 1)x. π 2n + 1 n= n= 7. 1 π sin x 2 cos 2nx. 8. Функцию следует продолжить следующим образом: f(x) = f(x), f(π x) = f(x), π 4n 2 1 то есть на промежутке [, π], график функции f(x) будет симметричен относительно вертикальной прямой x = π/2, на промежутке [, π] ее график центрально симметричен относительно точки (,). 23
24 2. Розкладання функції, заданої в проміжку [, π], тільки по синусах або тільки по косинусам Нехай функція f задана в проміжку [, π]. Бажаючи розкласти її в цьому проміжку в ряд Фур'є, ми спочатку продовжимо f в проміжок [, π] довільним чином, а потім скористаємося формулами Ейлера Фур'є. Свавілля в продовженні функції призводить до того, що для однієї і тієї ж функції f: [, π] R ми можемо отримувати різні ряди Фур'є. Але можна використовувати цю сваволю так, щоб отримати розкладання тільки по синусах або тільки по косинусам: в першому випадку достатньо продовжити f непарних чином, а по-другому парних. Алгоритм рішення 1. Продовжити функцію непарних (парних) чином на (,), а потім періодично з періодом 2π продовжити функцію на всю вісь. 2. Обчислити коефіцієнти Фур'є. 3. Скласти ряд Фур'є функції f (x). 4. Перевірити умови збіжності ряду. 5. Вказати функцію, до якої буде сходитися цей ряд. ПРИКЛАД 7. Розкладемо функцію f (x) \u003d cosx,< x < π, в ряд Фурье только по синусам. Решение. Продолжим функцию нечетным образом на (,) (т. е. так, чтобы равенство f(x) = f(x) выполнялось для всех x (, π)), а затем периодически с периодом 2π на всю ось. Получим функцию f (x), график которой приведен на рис
25 Рис. 17. Графік продовженої функції Очевидно, що функція f (x) кусочно-гладка. Обчислимо коефіцієнти Фур'є: a n \u003d для всіх n тому, що функція f (x) непарна. Якщо n 1, то bn \u003d 2 π f (x) sin πnxdx \u003d 2 π cosx sin nxdx \u003d \u003d 2 π dx \u003d \u003d 2 π cos (n + 1) x cos (n 1) x + \u003d π n + 1 n 1 \u003d 1 (1) n (1) n 1 1 \u003d π n + 1 n 1 \u003d 1, якщо n \u003d 2 k + 1, (1) n + 1 (n 1) + (n + 1) \u003d π ( n + 1) (n 1) 2 2n, якщо n \u003d 2k. π n 2 1 При n \u003d 1 в попередніх обчисленнях знаменник звертається в нуль, тому коефіцієнт b 1 обчислимо непосред- 25
26 ного: b 1 \u003d 2 π cosx sin xdx \u003d. Складемо ряд Фур'є функції f (x): f (x) 8 π k \u003d 1 k 4k 2 1 sin 2kx. Оскільки функція f (x) кусочно-гладка, то по теоремі про поточечной збіжності ряд Фур'є функції f (x) сходиться до суми: cosx, якщо π< x <, S(x) =, если x =, x = ±π, cosx, если < x < π. В результате функция f(x) = cosx, заданная на промежутке (, π), выражена через синусы: cosx = 8 π k=1 k 4k 2 1 sin 2kx, x (, π). Рис демонстрируют постепенное приближение частичных сумм S 1 (x), S 2 (x), S 3 (x) к разрывной функции f (x). 26
27 Рис. 18. Графік функції f (x) з накладеним на нього графіком часткової суми S 1 (x) Рис. 19. Графік функції f (x) з накладеним на нього графіком часткової суми S 2 (x) 27
28 Рис. 2. Графік функції f (x) з накладеним на нього графіком часткової суми S 3 (x) На рис. 21 наведені графіки функції f (x) і її часткової суми S 99 (x). Мал. 21. Графік функції f (x) з накладеним на нього графіком часткової суми S 99 (x) 28
29 ПРИКЛАД 8. Розкладемо функцію f (x) \u003d e ax, a\u003e, x [, π], в ряд Фур'є тільки по косинусам. Рішення. Продовжимо функцію парних чином на (,) (т. Е. Так, щоб рівність f (x) \u003d f (x) виконувалося для всіх x (, π)), а потім періодично з періодом 2π на всю числову вісь. Отримаємо функцію f (x), графік якої представлений на рис. 22. Функція f (x) в точках Рис. 22. Графік продовженої функції f (x) x \u003d kπ, k ціле число, має злами. Обчислимо коефіцієнти Фур'є: b n \u003d, так як f (x) парна. Інтегруючи по частинах отримуємо 29
30 an \u003d 2 π a \u003d 2 π \u003d 2 cosnxd (e ax) \u003d 2 πa e ax dx \u003d 2 π a (eaπ 1), f (x) cos πnxdx \u003d 2 π πa eax cosnx \u003d 2 πa (eaπ cosnπ 1 ) + 2n πa 2 π e ax cos nxdx \u003d + 2n e ax sin nxdx \u003d πa sin nxde ax \u003d \u003d 2 π a (eaπ cos n π 1) + 2n π sin nx π a 2eax 2n2 e ax cos nxdx \u003d 2 π a 2 π a (eaπ cos n π 1) n2 aa n. 2 Отже, a n \u003d 2a e aπ cos n π 1. π a 2 + n 2 Оскільки f (x) неперервна, то відповідно до теореми про поточечной збіжності її ряд Фур'є сходиться до f (x). Значить, для всіх x [, π] маємо f (x) \u003d 1 π a (eaπ 1) + 2a π k \u003d 1 e aπ (1) k 1 a 2 + k 2 coskx (x π). Рис демонструють поступове наближення часткових сум ряду Фур'є до заданої розривної функції. 3
31 Рис. 23. Графіки функцій f (x) і S (x) Рис. 24. Графіки функцій f (x) і S 1 (x) Рис. 25. Графіки функцій f (x) і S 2 (x) Рис. 26. Графіки функцій f (x) і S 3 (x) 31
32 Рис. 27. Графіки функцій f (x) і S 4 (x) Рис. 28. Графіки функцій f (x) і S 99 (x) ЗАВДАННЯ 9. Розкладіть функцію f (x) \u003d cos x, x π, в ряд Фур'є тільки по косинусам. 1. Розкладіть функцію f (x) \u003d e ax, a\u003e, x π, в ряд Фур'є тільки по синусах. 11. Розкладіть функцію f (x) \u003d x 2, x π, в ряд Фур'є тільки по синусах. 12. Розкладіть функцію f (x) \u003d sin ax, x π, в ряд Фур'є по тільки косинусам. 13. Розкладіть функцію f (x) \u003d x sin x, x π, в ряд Фур'є тільки по синусах. Відповіді 9. cosx \u003d cosx. 1. e ax \u003d 2 [1 (1) k e aπ] k sin kx. π a 2 + k2 k \u003d 1 11. x 2 2 [π 2 (1) n 1 π n + 2] n 3 ((1) n 1) sin nx. 32
33 12. Якщо a не є цілим числом, то sin ax \u003d 1 cosaπ (1 + + 2a cos 2nx) + π a 2 (2n) 2 + 2a 1 + cosaπ cos (2n 1) x π a 2 (2n 1) 2; якщо a \u003d 2m парне число, то sin 2mx \u003d 8m cos (2n 1) x π (2m) 2 (2n 1) 2; якщо a \u003d 2m 1 позитивне непарне число, то sin (2m 1) x \u003d 2 (cos 2nx) 1 + 2 (2m 1). π (2m 1) 2 (2n) π 16 n sin x sin 2nx. 2 π (4n 2 1) 2 3. Ряд Фур'є функції з довільним періодом Припустимо, що функція f (x) задана в проміжку [l, l], l\u003e. Зробивши підстановку x \u003d ly, y π, отримаємо функцію g (y) \u003d f (ly / π), визначену в проміжку π [, π]. Ця функція g (y) відповідає (формальний) ряд Фур'є () ly f \u003d g (y) a π 2 + (an cosny + bn sin ny), коефіцієнти якого знаходяться за формулами Ейлера Фур'є: an \u003d 1 π g (y) cosny dy \u003d 1 π f (ly π) cos ny dy, n \u003d, 1, 2, ..., 33
34 bn \u003d 1 π g (y) sinny dy \u003d 1 π f () ly sin ny dy, n \u003d 1, 2, .... π Повертаючись до старої змінної, т. Е. Вважаючи в виписаних формулах y \u003d πx / l, ми отримаємо для функції f (x) тригонометричний ряд кілька зміненого вигляду: де f (x) a 2 + an \u003d 1 lbn \u003d 1 lllll (an cos πnx lf (x) cos πnx lf (x) sin πnx l + bn sin πnx), (11) l dx, n \u003d, 1, 2, ..., (12) dx, n \u003d 1, 2, .... (13) Кажуть, що формули (11) (13) задають розкладання в ряд Фур'є функції з довільним періодом. ПРИКЛАД 9. Знайдемо ряд Фур'є функції, заданої в проміжку (l, l) виразом (A, якщо l< x, f(x) = B, если < x < l, считая, что она периодична с периодом 2l. Решение. Продолжим функцию периодически, с периодом 2l, на всю ось. Получим функцию f (x), кусочно-постоянную в промежутках (l + 2kl, l + 2kl), и претерпевающую разрывы первого рода в точках x = lk, k целое число. Ее коэффициенты Фурье вычисляются по формулам (12) и (13): 34
35 a \u003d 1 llf (x) dx \u003d 1 l A dx + 1 ll B dx \u003d A + B, llan \u003d 1 lllf (x) cos πnx l dx \u003d \u003d 1 l \u003d 1 ll A cos πnx l \u003d A + B π nlbn \u003d 1 l dx + 1 ll B cos πnx l sin πn \u003d, якщо n, ll A sin πnx lf (x) sin πnx l dx + 1 ll dx \u003d B sin πnx l \u003d BA (1 cosπn). πn Складемо ряд Фур'є функції f (x): f (x) A + B π (B A Так як cosπn \u003d (1) n, то n dx \u003d dx \u003d (1 cosπn) sin πnx). l при n \u003d 2k отримуємо b n \u003d b 2k \u003d, при n \u003d 2k 1 b n \u003d b 2k 1 \u003d 35 2 (B A) π (2k 1).
36 Звідси f (x) A + B (BA) π (sin πx + 1 3πx sin + 1 5πx sin + ... l 3 l 5 l Згідно з теоремою про поточечной збіжності ряд Фур'є функції f (x) сходиться до суми A, якщо l< x, S(x) = A + B, если x =, x = ±l, 2 B, если < x < l. Придавая параметрам l, A, B конкретные значения получим разложения в ряд Фурье различных функций. Пусть l = π, A =, B = 3π. На рис. 29 приведены графики первых пяти членов ряда, функции f (x) и частичной суммы S 7 (x) = a 2 + b 1 sin x b 7 sin 7x. Величина a является средним значением функции на промежутке. Обратим внимание на то, что с возрастанием ча- 2 стоты гармоники ее амплитуда уменьшается. Для наглядности графики трех высших гармоник сдвинуты по вертикали. На рис. 3 приведен график функции f(x) и частичной суммы S 99 (x) = a 2 + b 1 sin x b 99 sin 99x. Для наглядности на рис. 31 приведен тот же график в другом масштабе. Последние два графика иллюстрируют явление Гиббса. 36).
37 Рис. 29. Графік функції f (x) з накладеними на нього графіками гармонік S (x) \u003d a 2 і S 1 (x) \u003d b 1 sinx. Для наочності графіки трьох вищих гармонік S 3 (x) \u003d b 3 sin 3πx, S l 5 (x) \u003d b 5 sin 5πx l і S 7 (x) \u003d b 7 sin 7πx зрушені по вертикалі вгору l 37
38 Рис. 3. Графік функції f (x) з накладеним на нього графіком часткової суми S 99 (x) Рис. 31. Фрагмент рис. 3 в іншому масштабі 38
39 ЗАВДАННЯ В задачах розкласти в ряди Фур'є зазначені функції в заданих проміжках. 14. f (x) \u003d x 1, (1, 1). 15. f (x) \u003d ch2x, (2, 2] f (x) \u003d x (1 x), (1, 1]. 17. f (x) \u003d cos π x, [1, 1] f (x ) \u003d sin π x, (1, 1). (2 1, якщо 1< x < 1, 19. f(x) = 2l = 4., если 1 < x < 3; x, если x 1, 2. f(x) = 1, если 1 < x < 2, 2l = 3. { 3 x, если 2 x < 3;, если ωx, 21. f(x) = 2l = 2π/ω. sin ωx, если ωx π; Разложить в ряды Фурье: а) только по косинусам; б) только по синусам указанные функции в заданных промежутках (, l) { 22. f(x) = { 23. f(x) = ax, если < x < l/2, a(l x), если l/2 < x < l. 1, если < x 1, 2 x, если 1 x 2. Ответы 14. f(x) = 4 cos(2n 1)πx. π 2 (2n 1) f(x) = sh sh4 (1) n nπx cos 16 + π 2 n f(x) = cos 2nπx. π 2 n f(x) = 2 π + 8 π (1) n n 1 4n 2 cosnπx. 39
40 18. f (x) \u003d 8 (1) n n sin nπx. π 1 4n (1) n 2n + 1 cos πx. π 2n πn 2πnx π 2 sin2 cos n π sin ωx 2 cos 2nωx π 4n 2 1. (l 22. а) f (x) \u003d al 4 2) 1 (4n 2) πx cos, π 2 (2n 1) 2 l б) f (x) \u003d 4al (1) n 1 (2n 1) πx sin. π 2 (2n 1) 2 l 23. а) f (x) \u003d (cos π π 2 2 x 2 2 cos 2π 2 2 x cos 3π 2 2 x cos 5π), 2 2 x ... б) f ( x) \u003d 4 (sin π π 2 2 x 1 3 sin 3π) + 2 2 x (sin π π 2 x cos 2π) 2 x Комплексна форма ряду Фур'є Розкладання f (x) \u003d cne inx, де cn \u003d 1 2π f (x) e inx dx, n \u003d ± 1, ± 2, ..., називається комплексною формою ряду Фур'є. Функція розкладається в комплексний ряд Фур'є при виконанні тих же умов, при яких вона розкладається в речовинний ряд Фур'є. 4
41 ПРИКЛАД 1. Знайдемо ряд Фур'є в комплексній формі функції, заданої формулою f (x) \u003d e ax, в проміжку [, π), де a дійсне число. Рішення. Обчислимо коефіцієнти: \u003d c n \u003d 1 2π f (x) e inx dx \u003d 1 2π e (a in) x dx \u003d 1 ((1) n e aπ (1) n e aπ) \u003d (1) n sh aπ. 2π (a in) π (a in) Комплексний ряд Фур'є функції f має вигляд f (x) sh aπ π n \u003d (1) n a in einx. Переконаємося, що функція f (x) є кусково-гладкою: в проміжку (, π) вона безперервно-дифференцируема, і в точках x \u003d ± π існують кінцеві межі (5), (6) lim h + ea (+ h) \u003d e aπ, lim h + ea (π h) \u003d e aπ, ea (+ h) ea (+) lim h + h \u003d ae aπ ea (π h) ea (π), lim h + h \u003d ae aπ. Отже, функція f (x) представима поруч Фур'є sh aπ π n \u003d (1) n a in einx, який сходиться до суми: (e S (x) \u003d ax, якщо π< x < π, ch a, если x = ±π. 41
42 ПРИКЛАД 11. Знайдемо ряд Фур'є в комплексній і речової формі функції, заданої формулою f (x) \u003d 1 a 2 1 2a cosx + a2, де a< 1, a R. Решение. Функция f(x) является четной, поэтому для всех n b n =, а a n = 2 π f(x) cosnxdx = 2 (1 a2) π cos nxdx 1 2a cosx + a 2. Не будем вычислять такой сложный интеграл, а применим следующий прием: 1. используя формулы Эйлера sin x = eix e ix 2i = z z 1, cosx = eix + e ix 2i 2 = z + z 1, 2 где z = e ix, преобразуем f(x) к рациональной функции комплексной переменной z; 2. полученную рациональную функцию разложим на простейшие дроби; 3. разложим простейшую дробь по формуле геометрической прогрессии; 4. упростим полученную формулу. Итак, по формулам Эйлера получаем = f(x) = 1 a 2 1 a(z + z 1) + a 2 = (a 2 1)z (z a)(z a 1) = a z a az. (14) 42
43 Нагадаємо, що сума нескінченної геометричної прогресії зі знаменником q (q< 1) вычисляется по формуле: + n= q n = 1 1 q. Эта формула верна как для вещественных, так и для комплексных чисел. Поскольку az = a < 1 и a/z = a < 1, то az = + a n z n = a n e inx, a z a = a z 1 1 a/z = a z n= + n= a n z = + n n= n= a n+1 z = + a n+1 e i(n+1)x. n+1 После замены переменной (n + 1) = k, < k < 1, получим: 1 a z a = a k e ikx. Следовательно, f(x) + n= k= c n e inx, где c n = n= { a n, если n, a n, если n <, то есть c n = a n. Поскольку функция f(x) непрерывна, то в силу теоремы о поточечной сходимости имеет место равенство: f(x) = + n= a n e inx. Тем самым мы разложили функцию f(x) в ряд Фурье в комплексной форме. 43
44 А тепер знайдемо ряд Фур'є в речовій формі. Для цього згрупуємо доданки з номерами n і n для n: a n e inx + a n e inx \u003d 2a neinx + e inx Оскільки c \u003d 1, то 2 \u003d 2a n cos nx. f (x) \u003d 1 a 2 1 2a cosx + a \u003d a n cosnx. 2 Це ряд Фур'є в речовій формі функції f (x). Таким чином, не зрозумівши жодного інтеграла, ми знайшли ряд Фур'є функції. При цьому ми вирахували важкий інтеграл, що залежить від параметра cos nxdx 1 2a cosx + a \u003d 2 π an 2 1 a2, a< 1. (15) ПРИМЕР 12. Найдем ряд Фурье в комплексной и вещественной форме функции, заданной формулой a sin x f(x) = 1 2a cosx + a2, a < 1, a R. Решение. Функция f(x) является нечетной, поэтому для всех n a n = и b n = 2 π f(x) sin nxdx = 2a π sin x sin nxdx 1 2a cosx + a 2. Чтобы записать ряд Фурье нужно вычислить сложные интегралы или воспользоваться приемом, описанным выше. Поступим вторым способом: 44
45 a (zz 1) f (x) \u003d 2i (1 a (zz 1) + a 2) \u003d i 2 + i (a + a 1) z 2 2 (za) (za 1) \u003d \u003d i 2 + i () a 2 za + a 1. za 1 Кожну з простих дробів розкладемо по формулі геометричної прогресії: + aza \u003d a 1 z 1 a \u003d aanzzn, n \u003d za 1 za \u003d az \u003d anz n. n \u003d Це можливо, тому що az \u003d a / z \u003d a< 1. Значит + ia n /2, если n <, f(x) c n e inx, где c n =, если n =, n= ia n /2, если n >, Або, більш коротко, c n \u003d 1 2i a n sgnn. Тим самим, ряд Фур'є в комплексній формі знайдений. Згрупувавши доданки з номерами n і n отримаємо ряд Фур'є функції в речовій формі: \u003d f (x) \u003d + a sin x 1 2a cosx + a + 2 (1 2i an e inx 1 2i an e inx n \u003d +) \u003d cne inx \u003d an sin nx. Знову нам вдалося обчислити наступний складний інтеграл: sin x sin nxdx 1 2a cosx + a 2 \u003d π an 1. (16) 45
46 ЗАВДАННЯ 24. Використовуючи (15), обчисліть інтеграл cos nxdx 1 2a cosx + a 2 для речових a, a\u003e Використовуючи (16), обчисліть інтеграл sin x sin nxdx для речових a, a\u003e a cosx + a2 У завданнях знайдіть ряди Фур'є в комплексній формі для функцій. 26. f (x) \u003d sgn x, π< x < π. 27. f(x) = ln(1 2a cosx + a 2), a < 1. 1 a cosx 28. f(x) = 1 2a cosx + a2, a < Докажите, что функция f, определенная в промежутке [, π], вещественнозначна, если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является четной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n = ±1, ±2, Докажите, что функция f, определенная в промежутке [, π], является нечетной (т. е. удовлетворяет соотношению f(x) = f(x)), если и только если коэффициенты c n ее комплексного ряда Фурье связаны соотношениями c n = c n, n =, ±1, ±2,.... Ответы 1 2π 24. a n a π a n i + e 2inx, где подразумевается, что слагаемое, соответствующее n =, пропущено. π n n= a n n cosnx. 28. a n cosnx. n= 46
47 5. Рівність Ляпунова Теорема (рівність Ляпунова). Нехай функція f: [, π] R така, що f 2 (x) dx< +, и пусть a n, b n ее коэффициенты Фурье. Тогда справедливо равенство, a (a 2 n + b2 n) = 1 π называемое равенством Ляпунова. f 2 (x) dx, ПРИМЕР 13. Напишем равенство Ляпунова для функции { 1, если x < a, f(x) =, если a < x < π и найдем с его помощью суммы числовых рядов + sin 2 na n 2 и + Решение. Очевидно, 1 (2n 1) 2. 1 π f 2 (x) dx = 1 π a a dx = 2a π. Так как f(x) четная функция, то для всех n имеем b n =, a = 2 π f(x) dx = 2 π a dx = 2a π, 47
48 a n \u003d 2 π f (x) cosnxdx \u003d 2 π a cos nxdx \u003d 2 sin na πn. Тому рівність Ляпунова для функції f (x) набуває вигляду: 2 a 2 π + 4 sin 2 na \u003d 2a 2 π 2 n 2 π. З останнього рівності для a π знаходимо sin 2 na n 2 \u003d a (π a) 2 Вважаючи a \u003d π 2, отримуємо sin2 na \u003d 1 при n \u003d 2k 1 і sin 2 na \u003d при n \u003d 2k. Отже, k \u003d 1 1 (2k 1) 2 \u003d \u003d π2 8. ПРИКЛАД 14. Напишемо рівність Ляпунова для функції f (x) \u003d x cosx, x [, π], і знайдемо з його допомогою суму числового ряду (4n 2 + 1) 2 (4n 2 1) 4. 1 π Рішення. Прямі обчислення дають \u003d π π f 2 (x) dx \u003d 1 π x 2 cos 2 xdx \u003d 1 π x sin 2xdx \u003d π π x cos x \u003d π x 21 + cos 2x dx \u003d 2 π 1 4π cos 2xdx \u003d
49 Оскільки f (x) парна функція, то для всіх n маємо bn \u003d, an \u003d 2 π \u003d 1 π 1 \u003d π (n + 1) \u003d f (x) cosnxdx \u003d 2 π 1 cos (n + 1) x π (n + 1) 2 x cosxcosnxdx \u003d x (cos (n + 1) x + cos (n 1) x) dx \u003d 1 π sin (n + 1) xdx sin (n 1) xdx \u003d π (n 1) π π 1 + cos (n 1) x \u003d π (n 1) 2 1 (\u003d (1) (n + 1) 1) 1 (+ (1) (n + 1) 1) \u003d π (n + 1) 2 π (n 1) 2 () \u003d (1) (n + 1) 1 1 π (n + 1) + 1 \u003d 2 (n 1) 2 \u003d 2 (1) (n + 1) 1 nk π (n 2 1) \u003d π (4k 2 1) 2, якщо n \u003d 2k, 2, якщо n \u003d 2k + 1. Коефіцієнт a 1 необхідно обчислити окремо, оскільки в загальній формулі при n \u003d 1 знаменник дробу звертається в нуль. \u003d 1 π a 1 \u003d 2 π f (x) cosxdx \u003d 2 π x (1 + cos 2x) dx \u003d π 2 1 2π 49 x cos 2 xdx \u003d sin 2xdx \u003d π 2.
50 Таким чином, рівність Ляпунова для функції f (x) має вигляд: 8 π + π (4n 2 + 1) 2 π 2 (4n 2 1) \u003d π, звідки знаходимо суму числового ряду (4n 2 + 1) 2 (4n 2 1) \u003d π π ЗАВДАННЯ 32. Напишіть рівність Ляпунова для функції (xf (x) \u003d 2 πx, якщо x< π, x 2 πx, если π < x. 33. Напишите равенства Ляпунова для функций f(x) = cos ax и g(x) = sin ax, x [, π]. 34. Используя результат предыдущей задачи и предполагая, что a не является целым числом, выведите следующие классические разложения функций πctgaπ и (π/ sin aπ) 2 по рациональным функциям: πctgaπ = 1 a + + 2a a 2 n 2, (π) = sin aπ (a n) 2. n= 35. Выведите комплексную форму обобщенного равенства Ляпунова. 36. Покажите, что комплексная форма равенства Ляпунова справедлива не только для вещественнозначных функций, но и для комплекснозначных функций. 5
51 π (2n + 1) \u003d π sin 2απ 2απ \u003d 2sin2 απ α 2 π 2 Відповіді + 4 sin2 απ π 2 α 2 (α 2 n 2) 2; sin 2απ 1 2απ \u003d απ n 2 4sin2 π 2 (α 2 n 2) 2. 1 π 35. f (x) g (x) dx \u003d cndn, де cn коефіцієнт Фур'є 2π функції f (x), а dn коефіцієнт Фур'є функції g (x). 6. Диференціювання рядів Фур'є Нехай f: R R безперервно диференціюється 2π-періодична функція. Її ряд Фур'є має вигляд: f (x) \u003d a 2 + (a n cos nx + b n sin nx). Похідна f (x) цієї функції буде безперервної і 2π-періодичною функцією, для якої можна записати формальний ряд Фур'є: f (x) a 2 + (an cos nx + bn sin nx), де a, an, bn, n \u003d 1 , 2, ... коефіцієнти Фур'є функції f (x). 51
52 Теорема (про почленного диференціюванні рядів Фур'є). При зроблених вище припущеннях справедливі рівності a \u003d, a n \u003d nb n, b n \u003d na n, n 1. ПРИКЛАД 15. Нехай кусочно-гладка функція f (x) неперервна в проміжку [, π]. Доведемо, що при виконанні умови f (x) dx \u003d має місце нерівність 2 dx 2 dx, зване нерівністю Стеклова, і переконаємося, що рівність в ньому здійснюється лише для функцій виду f (x) \u003d A cosx. Іншими словами, нерівність Стеклова дає умови, при виконанні яких з малості похідною (в среднеквадратичном) слід трохи функції (в среднеквадратичном). Рішення. Продовжимо функцію f (x) на проміжок [,] парних чином. Позначимо продовжену функцію тим же символом f (x). Тоді продовжена функція буде безперервної і кусочно-гладкою на відрізку [, π]. Так як функція f (x) неперервна, то f 2 (x) неперервна на відрізку і 2 dx< +, следовательно, можно применить теорему Ляпунова, согласно которой имеет место равенство 1 π 2 dx = a () a 2 n + b 2 n. 52
53 Так як продовжена функція парна, то b n \u003d, a \u003d за умовою. Отже, рівність Ляпунова набирає вигляду 1 π 2 dx \u003d a 2 π n. (17) Переконаємося, що для f (x) виконується висновок теореми про почленного диференціюванні ряду Фур'є, тобто що a \u003d, an \u003d nb n, bn \u003d na n, n 1. Нехай похідна f (x) зазнає злами в точках x 1, x 2, ..., x N в проміжку [, π]. Позначимо x \u003d, x N + 1 \u003d π. Розіб'ємо проміжок інтегрування [, π] на N +1 проміжок (x, x 1), ..., (x N, x N + 1), на кожному з яких f (x) неперервно диференційовна. Тоді, використовуючи властивість адитивності інтеграла, а потім інтегруючи по частинах, отримаємо: bn \u003d 1 π \u003d 1 π \u003d 1 π f (x) sin nxdx \u003d 1 π N f (x) sin nx j \u003d N f (x) sin nx j \u003d x j + 1 xjx j + 1 xjnn π N j \u003d x j + 1 xjx j + 1 xjf (x) sin nxdx \u003d f (x) cosnxdx \u003d f (x) cosnxdx \u003d \u003d 1 π [(f (x 1) sin nx 1 f (x) sin nx) + + (f (x 2) sinnx 2 f (x 1) sin nx 1)
54 + (f (x N + 1) sin nx N + 1 f (x N) sin nx N)] na n \u003d \u003d 1 π na n \u003d \u003d 1 π na n \u003d na n. x j + 1 a \u003d 1 f (x) dx \u003d 1 N f (x) dx \u003d π π j \u003d xj \u003d 1 N x j + 1 f (x) π \u003d 1 (f (π) f ()) \u003d . x j π j \u003d Остання рівність має місце в силу того, що функція f (x) була продовжена парних чином, а значить f (π) \u003d f (). Аналогічно отримаємо a n \u003d nb n. Ми показали, що теорема про почленного диференціюванні рядів Фур'є для безперервної кусочно-гладкою 2π-періодичної функції, похідна якої в проміжку [, π] зазнає розриви першого роду, вірна. Значить f (x) a 2 + (an cosnx + bn sin nx) \u003d (na n) sin nx, так як a \u003d, an \u003d nb n \u003d, bn \u003d na n, n \u003d 1, 2, .... оскільки 2 dx< +, то по равенству Ляпунова 1 π 2 dx = 54 n 2 a 2 n. (18)
55 Так як кожен член ряду в (18) більше або дорівнює відповідного члена ряду в (17), то 2 dx 2 dx. Згадуючи, що f (x) є парним продовженням вихідної функції, маємо 2 dx 2 dx. Що і доводить рівність Стеклова. Тепер досліджуємо для яких функцій у нерівності Стеклова має місце рівність. Якщо хоч для одного n 2, коефіцієнт a n відмінний від нуля, то a 2 n< na 2 n. Следовательно, равенство a 2 n = n 2 a 2 n возможно только если a n = для n 2. При этом a 1 = A может быть произвольным. Значит в неравенстве Стеклова равенство достигается только на функциях вида f(x) = A cosx. Отметим, что условие πa = f(x)dx = (19) существенно для выполнения неравенства Стеклова, ведь если условие (19) нарушено, то неравенство примет вид: a a 2 n n 2 a 2 n, а это не может быть верно при произвольном a. 55
56 ЗАВДАННЯ 37. Нехай кусочно-гладка функція f (x) неперервна в проміжку [, π]. Доведіть, що при виконанні умови f () \u003d f (π) \u003d має місце нерівність 2 dx 2 dx, також зване нерівністю Стеклова, і переконайтеся, що рівність в ньому має місце лише для функцій виду f (x) \u003d B sin x. 38. Нехай функція f неперервна в проміжку [, π] і має в ньому (за винятком хіба лише кінцевого числа точок) похідну f (x), інтегруються з квадратом. Доведіть, що якщо при цьому виконані умови f () \u003d f (π) і f (x) dx \u003d, то має місце нерівність 2 dx 2 dx, зване нерівністю Віртінгера, причому рівність в ньому має місце лише для функцій виду f (x ) \u003d A cosx + B sin x. 56
57 7. Застосування рядів Фур'є для розв'язання диференціальних рівнянь в приватних похідних При вивченні реального об'єкта (явища природи, виробничого процесу, системи управління і т. Д.) Істотними виявляються два фактори: рівень накопичених знань про досліджуваний об'єкт і ступінь розвитку математичного апарату. На сучасному етапі наукових досліджень виробилася наступна ланцюжок: явище фізична модель математична модель. Фізична постановка (модель) завдання полягає в наступному: виявляються умови розвитку процесу і головні чинники на нього впливають. Математична постановка (модель) полягає в описі обраних у фізичній постановці факторів і умов у вигляді системи рівнянь (алгебраїчних, диференціальних, інтегральних та ін.). Завдання називається коректно поставленої, якщо в певному функціональному просторі рішення задачі існує, єдино і безперервно залежить від початкових і граничних умов. Математична модель не буває тотожна даного об'єкту, а є його наближеним описом Висновок рівняння вільних малих поперечних коливань струни Будемо слідувати підручником. Нехай кінці струни закріплені, а сама струна туго натягнута. Якщо вивести струну з положення рівноваги (наприклад, відтягнути або вдарити по ній), то струна почне 57
58 коливатися. Будемо припускати, що всі крапки струни рухаються перпендикулярно її положення рівноваги (поперечні коливання), причому в кожен момент часу струна лежить в одній і тій же площині. Візьмемо в цій площині систему прямокутних координат xou. Тоді, якщо в початковий момент часу t \u003d струна розташовувалася уздовж осі Ox, то u означатиме відхилення струни від положення рівноваги, тобто, положення точки струни з абсцисою x в довільний момент часу t відповідає значення функції u (x, t). При кожному фіксованому значенні t графік функції u (x, t) являє форму коливається струни в момент часу t (рис. 32). При постійному значенні x функція u (x, t) дає закон руху точки з абсцисою x вздовж прямої, паралельної осі Ou, похідна u t швидкість цього руху, а друга похідна 2 u t 2 прискорення. Мал. 32. Сили, прикладені до нескінченно малому ділянці струни Складемо рівняння, якому повинна задовольняти функція u (x, t). Для цього зробимо ще кілька спрощують припущень. Будемо вважати струну абсолютно гинув- 58
59 кой, тобто будемо вважати, що струна не чинить опір вигину; це означає, що напруги, що виникають в струні, завжди спрямовані по дотичним до її миттєвому профілем. Струна передбачається пружною і підкоряється закону Гука; це означає, що зміна величини сили натягу пропорційно зміні довжини струни. Приймемо, що струна однорідна; це означає, що її лінійна щільність ρ постійна. Зовнішніми силами ми нехтуємо. Це і означає, що ми розглядаємо вільні коливання. Ми будемо вивчати тільки малі коливання струни. Якщо позначити через φ (x, t) кут між віссю абсцис і дотичній до струни в точці з абсцисою x в момент часу t, то умова малості коливань полягає в тому, що величиною φ 2 (x, t) можна нехтувати в порівнянні з φ (x, t), т. е. φ 2. Так як кут φ малий, то cosφ 1, φ sin φ tg φ u отже, величиною (uxx,) 2 також можна нехтувати. Звідси відразу випливає, що в процесі коливання можемо знехтувати зміною довжини будь-якої ділянки струни. Дійсно, довжина шматочка струни M 1 M 2, проектують в проміжок осі абсцис, де x 2 \u003d x 1 + x, дорівнює l \u003d x 2 x () 2 u dx x. x Покажемо, що при наших припущеннях величина сили натягу T буде постійною уздовж всієї струни. Візьмемо для цього будь-якої ділянку струни M 1 M 2 (рис. 32) в момент часу t і замінимо дію відкинутих участ- 59
60 ков силами натяжений T 1 і T 2. Оскільки за умовою всі точки струни рухаються паралельно осі Ou і зовнішні сили відсутні, то сума проекцій сил натягу на вісь Ox повинна дорівнювати нулю: T 1 cosφ (x 1, t) + T 2 cosφ (x 2, t) \u003d. Звідси в силу малості кутів φ 1 \u003d φ (x 1, t) і φ 2 \u003d φ (x 2, t) робимо висновок, що T 1 \u003d T 2. Позначимо загальне значення T 1 \u003d T 2 через T. Тепер обчислимо суму проекцій F u цих же сил на вісь Ou: F u \u003d T sin φ (x 2, t) T sin φ (x 1, t). (2) Так як для малих кутів sin φ (x, t) tg φ (x, t), а tg φ (x, t) u (x, t) / x, то рівняння (2) можна переписати так F u T (tg φ (x 2, t) tg φ (x 1, t)) (u T x (x 2, t) u) x (x 1, t) xx T 2 ux 2 (x 1, t) x . Так як точка x 1 вибрана довільно, то F u T 2 u x2 (x, t) x. Після того як знайдені всі сили, що діють на ділянку M 1 M 2, застосуємо до нього другий закон Ньютона, згідно з яким добуток маси на прискорення дорівнює сумі всіх діючих сил. Маса шматочка струни M 1 M 2 дорівнює m \u003d ρ l ρ x, а прискорення дорівнює 2 u (x, t). Рівняння t 2 Ньютона набирає вигляду: 2 u t (x, t) x \u003d u 2 α2 2 x2 (x, t) x, де α 2 \u003d T ρ постійне позитивне число. 6
61 Скорочуючи на x, отримаємо 2 u t (x, t) \u003d u 2 α2 2 x2 (x, t). (21) В результаті ми отримали лінійне однорідне диференціальне рівняння з приватними похідними другого порядку з постійними коефіцієнтами. Його називають рівнянням коливань струни або одновимірним хвильовим рівнянням. Рівняння (21) по суті є переформулюванням закону Ньютона і описує рух струни. Але в фізичної постановці завдання були присутні вимоги про те, що кінці струни закріплені і положення струни в якійсь момент часу відомо. Рівняннями ці умови будемо записувати так: а) будемо вважати, що кінці струни закріплені в точках x \u003d і x \u003d l, т. Е. Вважатимемо, що для всіх t виконані співвідношення u (, t) \u003d, u (l, t ) \u003d; (22) б) будемо вважати, що в момент часу t \u003d положення струни збігається з графіком функції f (x), т. Е. Вважатимемо, що для всіх x [, l] виконано рівність u (x,) \u003d f ( x); (23) в) будемо вважати, що в момент часу t \u003d точці струни з абсцисою x надана швидкість g (x), т. Е. Вважатимемо, що u (x,) \u003d g (x). (24) t Співвідношення (22) називаються граничними умовами, а співвідношення (23) і (24) називаються початковими умовами. Математична модель вільних малих поперечних 61
62 коливань струни полягає в тому, що треба вирішити рівняння (21) з граничними умовами (22) і початковими умовами (23) і (24) Рішення рівняння вільних малих поперечних коливань струни методом Фур'є Рішення рівняння (21) в області x l,< t <, удовлетворяющие граничным условиям (22) и начальным условиям (23) и (24), будем искать методом Фурье (называемым также методом разделения переменных). Метод Фурье состоит в том, что частные решения ищутся в виде произведения двух функций, одна из которых зависит только от x, а другая только от t. То есть мы ищем решения уравнения (21), которые имеют специальный вид: u(x, t) = X(x)T(t), (25) где X дважды непрерывно дифференцируемая функция от x на [, l], а T дважды непрерывно дифференцируемая функция от t, t >. Підставляючи (25) в (21), отримаємо: X T \u003d α 2 X T, (26) або T (t) α 2 T (t) \u003d X (x) X (x). (27) Кажуть, що відбувся поділ змінних. Так як x і t не залежать одне від одного, то ліва частина в (27) не залежить від x, а права від t і загальна величина цих відносин 62
63 повинна бути постійною, яку позначимо через λ: T (t) α 2 T (t) \u003d X (x) X (x) \u003d λ. Звідси отримуємо два звичайних диференціальних рівнянь: X (x) λx (x) \u003d, (28) T (t) α 2 λt (t) \u003d. (29) При цьому граничні умови (22) приймуть вигляд X () T (t) \u003d і X (l) T (t) \u003d. Оскільки вони повинні виконуватися для всіх t, t\u003e, то X () \u003d X (l) \u003d. (3) Знайдемо рішення рівняння (28), який задовольняє граничним умовам (3). Розглянемо три випадки. Випадок 1: λ\u003e. Позначимо λ \u003d β 2. Рівняння (28) набуває вигляду X (x) β 2 X (x) \u003d. Його характеристичне рівняння k 2 β 2 \u003d має коріння k \u003d ± β. отже, загальне рішення рівняння (28) має вигляд X (x) \u003d C e βx + De βx. Ми повинні підібрати постійні C і D так, щоб дотримувалися граничні умови (3), т. Е. X () \u003d C + D \u003d, X (l) \u003d C e βl + De βl \u003d. Оскільки β, то ця система рівнянь має єдине рішення C \u003d D \u003d. Отже, X (x) і 63
64 u (x, t). Тим самим, в разі 1 ми отримали тривіальне рішення, яке далі розглядати не будемо. Випадок 2: λ \u003d. Тоді рівняння (28) приймає вигляд X (x) \u003d і його рішення, очевидно, задається формулою: X (x) \u003d C x + d. Підставляючи це рішення в граничні умови (3), отримаємо X () \u003d D \u003d і X (l) \u003d Cl \u003d, значить, C \u003d D \u003d. Отже, X (x) і u (x, t), і ми знову отримали тривіальне рішення. Випадок 3: λ<. Обозначим λ = β 2. Уравнение (28) принимает вид: X (x)+β 2 X(x) =. Его характеристическое уравнение имеет вид k 2 + β 2 =, а k = ±βi являются его корнями. Следовательно, общее решение уравнения (28) в этом случае имеет вид X(x) = C sin βx + D cosβx. В силу граничных условий (3) имеем X() = D =, X(l) = C sin βl =. Поскольку мы ищем нетривиальные решения (т. е. такие, когда C и D не равны нулю одновременно), то из последнего равенства находим sin βl =, т. е. βl = nπ, n = ±1, ±2,..., n не равно нулю, так как сейчас мы рассматриваем случай 3, в котором β. Итак, если β = nπ (nπ) 2, l, т. е. λ = то существуют l решения X n (x) = C n sin πnx, (31) l C n произвольные постоянные, уравнения (28), не равные тождественно нулю. 64
65 Надалі будемо надавати n тільки позитивні значення n \u003d 1, 2, ..., оскільки при негативних n будуть виходити рішення того (ж виду. Nπ) Величини λ n \u003d називаються власними числами, а функції X n (x) \u003d C n sin πnx власними функ- ll ціями диференціального рівняння (28) з крайовими умовами (3). Тепер вирішимо рівняння (29). Для нього характеристичне рівняння має вигляд k 2 α 2 λ \u003d. (32) l 2 Оскільки вище ми з'ясували, що нетривіальні рішення X (x) рівняння (28) є тільки для негативних λ, рівних λ \u003d n2 π 2, то саме такі λ ми і будемо розглядати далі. Корінням рівняння (32) є k \u003d ± iα λ, а рішення рівняння (29) мають вигляд: T n (t) \u003d A n sin πnαt + B n cos πnαt, (33) l l де A n і B n довільні постійні. Підставляючи формули (31) і (33) в (25), знайдемо приватні рішення рівняння (21), задовольняють крайовим умовам (22): (un (x, t) \u003d B n cos πnαt + A n sin πnαt) C n sin πnx. lll Вносячи множник C n в дужку і вводячи позначення C n A n \u003d bn і B n C n \u003d an, запишемо un (X, T) у вигляді (un (x, t) \u003d an cos πnαt + bn sin πnαt) sin πnx. (34) l l l 65
66 Коливання струни, відповідні рішенням u n (x, t), називаються власними коливаннями струни. Так як рівняння (21) і граничні умови (22) лінійні і однорідні, то лінійна комбінація рішень (34) (u (x, t) \u003d an cos πnαt + bn sin πnαt) sin πnx (35) lll буде рішенням рівняння (21 ), що задовольняє граничним умовам (22) при спеціальному виборі коефіцієнтів an і bn, що забезпечує рівномірну збіжність ряду. Тепер підберемо коефіцієнти an і bn рішення (35) так, щоб воно задовольняло не тільки граничним, але і початкових умов (23) і (24), де f (x), g (x) задані функції (причому f () \u003d f (l) \u003d g () \u003d g (l) \u003d). Вважаємо, що функції f (x) і g (x) задовольняють умовам розкладання в ряд Фур'є. Підставляючи в (35) значення t \u003d, отримаємо u (x,) \u003d a n sin πnx l \u003d f (x). Диференціюючи ряд (35) по t і підставляючи t \u003d, отримаємо u t (x,) \u003d πnα b n sin πnx l l \u003d g (x), а це є розкладання функцій f (x) і g (x) в ряди Фур'є. Отже, a n \u003d 2 l l f (x) sin πnx l dx, b n \u003d 2 l g (x) sin πnx dx. πnα l (36) 66
67 Подставляявираженіядлякоеффіціентов a n і b n в ряд (35), ми отримаємо рішення рівняння (21), яке задовольняє граничним умовам (22) і початкових умов (23) і (24). Тим самим ми вирішили задачу про вільні малих поперечних коливаннях струни. З'ясуємо фізичний зміст власних функцій u n (x, t) завдання про вільні коливання струни, визначених формулою (34). Перепишемо її у вигляді де u n (x, t) \u003d α n cos πnα l α n \u003d a 2 n + b2 n, (t + δ n) sin πnx, (37) l πnα δ n \u003d arctg b n. l a n З формули (37) видно, що всі точки струни здійснюють гармонійні коливання з однією і тією ж частотою ω n \u003d πnα і фазою πnα δ n. Амплітуда коливання залежить від l l абсциси x точки струни і дорівнює α n sin πnx. При такому коливанні всі крапки струни одночасно досягають свого l максимального відхилення в ту або іншу сторону і одночасно проходять положення рівноваги. Такі коливання називаються стоячими хвилями. Стояча хвиля матиме n + 1 нерухому точку, що задається корінням рівняння sin πnx \u003d в проміжку [, l]. Нерухомі точки називаються вузлами стоячої хвилі. Посередині між узла- l ми розташовуються точки, в яких відхилення досягають максимуму; такі точки називаються пучностями. Кожна струна може мати власні коливання строго визначених частот ω n \u003d πnα, n \u003d 1, 2, .... Ці частоти називаються власними частотами струни. Найнижчий l тон, який може видавати струна, визначається самою 67
68 низькою власною частотою ω 1 \u003d π T і називається основним тоном струни. Решта тони, відповідні l ρ частотам ω n, n \u003d 2, 3, ..., називаються обертонами або гармоніками. Для наочності зобразимо типові профілі струни, яка видає основний тон (рис. 33), перший обертон (рис. 34) і другий обертон (рис. 35). Мал. 33. Профіль струни, яка видає основний тон Рис. 34. Профіль струни, яка видає перший обертон Рис. 35. Профіль струни, яка видає другий обертон Якщо струна здійснює вільні коливання, обумовлені початковими умовами, то функція u (x, t) представляється, як це видно з формули (35), у вигляді суми окремих гармонік. Таким чином довільне коливання 68
69 струни являє собою суперпозицію стоячих хвиль. При цьому характер звучання струни (тон, сила звуку, тембр) буде залежати від співвідношення між амплітудами окремих гармонік Сила, висота і тембр звуку Коливання струна збуджує коливання повітря, що сприймаються вухом людини як звук, що видається струною. Сила звуку характеризується енергією або амплітудою коливань: чим більше енергія, тим більше сила звуку. Висота звуку визначається його частотою або періодом коливань: чим більше частота, тим вище звук. Тембр звуку визначається наявністю обертонів, розподілом енергії по гармоникам, т. Е. Способом збудження коливань. Амплітуди обертонів, взагалі кажучи, менше амплітуди основного тону, а фази обертонів можуть бути довільними. Наше вухо не відчутно до фази коливань. Порівняйте, наприклад, дві криві на рис. 36, запозичений із. Це запис звуку з одним і тим же основним тоном, витягнутого з кларнета (а) і рояля (б). Обидва звуку не є простих синусоїдальних коливань. Основна частота звуку в обох випадках однакова це і створює однаковість тони. Але малюнки кривих різні тому, що на основний тон накладені різні обертони. В якомусь сенсі ці малюнки показують, що таке тембр. 69
Рівняння гіперболічного типу. Коливання нескінченної і полубесконечной струни. Метод Фур'є метод Фур'є Стоячі хвилі 4 Лекція 4.1 Рівняння гіперболічного типу. Коливання нескінченної і полубесконечной
МОСКОВСЬКИЙ ДЕРЖАВНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ цивільної авіації В.М. Любимов, Е.А. Жукова, В.А. Ухова, Ю.А. Шуринов М А Т Е М А Т И К А Р Я Д И ПОСІБНИК з вивчення дисципліни та контрольні завдання
Освіти та науки Росії Федеральне державне бюджетне освітня установа вищої професійної освіти МАТИ Російський державний технологічний університет імені К. Е. Ціолковського
Міністерство освіти Республіки Білорусь УО «Вітебський державний технологічний університет» Тема. «Ряди» Кафедра теоретичної і прикладної математики. розроблена доц. Є.Б. Дуніной. Основні
Федеральне агентство з освіти Федеральне державне освітня установа вищої професійної освіти ПІВДЕННИЙ федеральний університет Р. М. Гаврилова, Г. С. Костецька Методичні
Тема Ряди Фур'є Практичне заняття Ряди Фур'є по ортогональним системам функцій Простір кусочно-безперервних функцій Узагальнений ряд Фур'є 3 Нерівність Бесселя і збіжність ряду Фур'є Простір
ТЕОРІЯ РЯДОВ Теорія рядів є найважливішою складовою частиною математичного аналізу і знаходить як теоретичні, так і численні практичні додатки. Розрізняють ряди числові і функціональні.
ЗМІСТ ЛАВИ ФУР'Е 4 Поняття про періодичну функції 4 Тригонометричний поліном 6 3 Ортогональні системи функцій 4 Тригонометричний ряд Фур'є 3 5 Ряд Фур'є для парних і непарних функцій 6 6 Розкладання
Федеральне агентство з освіти Московський Державний університет геодезії і картографії (МІІГАіК) Методичні вказівки І ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ з курсу ВИЩА МАТЕМАТИКА Числові
Лекція 4. Гармонійний аналіз. Ряди Фур'є Періодичні функції. Гармонійний аналіз В науці і техніці часто доводиться мати справу з періодичними явищами, т. Е. Такими, які повторюються через
ТЕМА V РЯД ФУР'Е Лекція 6 Розкладання періодичної функції в ряд Фур'є Багато процесів відбуваються в природі і техніці мають властивості повторюватися через певні проміжки часу Такі процеси
Методичні вказівки до розрахункового завдання з курсу ВИЩОЇ МАТЕМАТИКИ «ЗВИЧАЙНІ ДИФЕРЕНЦІАЛЬНІ РІВНЯННЯ ЛАВИ ПОДВІЙНЕ інтеграли» ЧАСТИНА Ш ТЕМА ЛАВИ Зміст Ряди Числові ряди Збіжність і розбіжність
6 Ряди Фур'є 6 Ортогональні системи функцій Ряд Фур'є по ортогональній системі функцій Функції φ () і ψ (), певні і інтегровані на відрізку [,], називаються ортогональними на цьому відрізку, якщо
ВИЗНАЧЕНИЙ ІНТЕГРАЛ. Інтегральні суми і певний інтеграл Нехай дана функція y \u003d f (), певна на відрізку [, b], де< b. Разобьём отрезок [, b ] с помощью точек деления на n элементарных
5 Статечні ряди 5 Статечні ряди: визначення, область збіжності Функціональний ряд виду (a + a) + a () + K + a () + K a) (, (5) де, a, a, K, a, k деякі числа, називають статечним рядом числа
Білоруський державний університет ФАКУЛЬТЕТ ПРИКЛАДНОЇ МАТЕМАТИКИ ТА ІНФОРМАТИКИ Кафедра вищої математики Навчально-методичний посібник для студентів факультету прикладної математики та інформатики
Розглянемо деякі приклади. Приклад. Знайдемо суму нескінченної геометричної прогресії Формула загального члена цього ряду a + aq + ... + aq n + ... (a). a n \u003d aq n. Обчислимо його часткові суми. Якщо q \u003d, то
Завдання 1.1. Знайти в зазначеній галузі відмінні від тотожного нуля рішення y \u003d y (x) диференціального рівняння, що задовольняють заданим крайовим умовам (завдання Штурма-Ліувілля) Рішення: Розглянемо
Математичний аналіз Тема: Визначений інтеграл Невласні інтеграли Лектор Пахомова Є.Г. 2017 р ГЛАВА II. Визначений інтеграл та його застосування 1. Визначений інтеграл і його властивості 1. Завдання,
Лекція 8 4 Завдання Штурма-Ліувілля Розглянемо початково-крайову задачу для диференціального рівняння в приватних похідних другого порядку описує малі поперечні коливання струни Струна розглядається
Пояснення до тексту: знак читається як "рівносильно" і позначає, що у рівнянь праворуч від знака і зліва від знака безліч рішень збігається, знак IR позначає ммножество дійсних чисел, знак IN
82 4. Розділ 4. Функціональні і статечні ряди 4.2. Заняття 3 4.2. Заняття 3 4.2 .. Розкладання функції в ряд Тейлора ВИЗНАЧЕННЯ 4.2 .. Нехай функція y \u003d f (x) нескінченно диференційована в деякому околі
Освіти та науки Росії Федерального державного БЮДЖЕТНА освітня установа вищої професійної освіти «САМАРСЬКИЙ державний технічний університет» К а ф е д р а Прикладної математики
Федеральне агентство залізничного транспорту Уральський державний університет шляхів сполучення Кафедра «Вища і прикладна математика» Н. П. Чуєв Елементи гармонійного аналізу Методичні
Лекція 3 Ряди Тейлора і Маклорена Застосування степеневих рядів Розкладання функцій в статечні ряди Ряди Тейлора і Маклорена Для додатків важливо вміти цю функцію розкладати в статечної ряд, ті функцію
З А Лавренченко wwwwrckoru Лекція Перетворення Фур'є Поняття інтегрального перетворення Метод інтегральних перетворень один з потужних методів математичної фізики є потужним засобом вирішення
Интегрируемость функції (за Ріманом) і певний інтеграл Приклади розв'язання задач 1. Постійна функція f (x) \u003d C интегрируема, так як для будь-яких розбиття і будь-якого вибору точок ξ i інтегральні
I курс, завдання. Доведіть, що функція Рімана, якщо 0, m m R (), якщо, m, m 0, і дріб нескоротних, 0, якщо ірраціонально, розривна в кожній раціональної точки і неперервна в кожній ірраціональної. Рішення.
1 2 Зміст 1 Ряди Фур'є 5 1.1 Тригонометричний ряд Фур'є ............ 5 1.2 Тільки sin & cos ..................... 7 1.3 Ряд Фур'є в комплексній формі ........... 11 1.4 f (x) \u003d ck? .......................
Рівняння математичної фізики 1. Диференціальні рівняння з приватними похідними Рівняння, що зв'язує невідому функцію u (x 1, x 2, ..., x n), незалежні змінні x 1, x 2, ..., x n і приватні
Лекція 4. Хвильові рівняння 1. Висновок рівняння коливань струни 2. Рівняння поздовжніх коливань стрижня 3. Початкові умови, крайові умови 4. Постановка задач 1. Висновок рівняння коливань струни
1. Електростатика 1 1. Електростатика Урок 6 Поділ змінних в декартових координатах 1.1. (Завдання 1.49) Площина z \u003d заряджена з щільністю σ (x, y) \u003d σ sin (αx) sin (βy), де σ, α, β постійні.
Модуль Тема Функціональні послідовності і ряди Властивості рівномірної збіжності послідовностей і рядів Статечні ряди Лекція Визначення функціональних послідовностей і рядів Рівномірно
Рівнянням параболічного типу. Метод розділення змінних Однорідна крайова задача Функція джерела Неоднорідне рівняння теплопровідності 7 Лекція 7.1 рівнянь параболічного типу. метод поділу
Лекція Числові ряди Ознаки збіжності Числові ряди Ознаки збіжності Нескінченне вираз числової послідовності + + + +, складене з членів нескінченної, називається числовим рядом Числа,
35 7 Тригонометричні ряди Фур'є Ряди Фур'є для періодичних функцій з періодом T. Нехай f (x) - кусочно - безперервна періодична функція з періодом T. Розглянемо основну тригонометричну систему
Металургійний факультет Кафедра вищої математики ЛАВИ Методичні вказівки Новокузнецьк 5 Федеральне агентство з освіти Державна освітня установа вищої професійної освіти
Кафедра математики та інформатики Елементи вищої математики Навчально-методичний комплекс для студентів СПО, що навчаються із застосуванням дистанційних технологій Модуль Диференціальне числення Укладач:
9. Первісна та невизначений інтеграл 9 .. Нехай на проміжку I R задана функція f (). Функцію F () називають первісної функції f () на проміжку I, якщо F () \u003d f () для будь-якого I, і первісної
ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЮ Поняття похідної, її геометричний і фізичний зміст Завдання, що призводять до поняття похідної Визначення Дотичній S до лінії y f (x) в точці A x; f (
Рівняння гіперболічного типу. Коливання нескінченної і полубесконечной струни. Метод Даламбера Нескінченна струна. Формула Даламбера напівнескінченної струна 3 Лекція 3.1 Рівняння гіперболічного типу.
Зміст Введення. Основні поняття .... 4 1. Інтегральні рівняння Вольтерри ... 5 Варіанти домашніх завдань .... 8 2. резольвенту інтегрального рівняння Вольтерри. 10 Варіанти домашніх завдань .... 11
ЛАВ. Числові ряди. Основні визначення Нехай дана нескінченна послідовність чисел Вираз (нескінченна сума) a, a 2, ..., a n, ... a i \u003d a + a 2 + + a n + ... () i \u003d називається числовим рядом. числа
8. Статечні ряди 8 .. Функціональний ряд виду c n (z) n, (8.) n \u003d де c n числова послідовність, R фіксоване число, а z R, називають статечним поруч з коефіцієнтами c n. Виконавши заміну змінних
~ ~ Невизначений і визначений інтеграли Поняття первісної та неопределѐнного інтеграла. Означення: Функція F називається первісною по відношенню до функції f, якщо ці функції пов'язані наступним
3724 ЛАВ кратні і криволінійні інтеграли 1 РОБОЧА ПРОГРАМА РОЗДІЛІВ «ЛАВ кратні і криволінійні інтеграли» 11 Числові ряди Поняття числового ряду Властивості числових рядів Необхідна ознака збіжності
Е.М. РУДІЙ МАТЕМАТИЧНИЙ АНАЛІЗ. ЧИСЛОВІ І ФУНКЦІОНАЛЬНІ РЯДИ НОВОСИБИРСК 200 2 освіти та науки Росії ГОУ ВПО «Новосибірський державний педагогічний університет» Е.М. Рудой МАТЕМАТИЧНИЙ АНАЛІЗ.
Лекція N 7. Статечні ряди і ряди Тейлора..Степенние ряди ..... Ряд Тейлора .... 4.Разложеніе деяких елементарних функцій в ряди Тейлора і Маклорена .... 5 4.Применение статечних рядів .... 7 .Ступінь
КВАДРАТНІ Рівняння Зміст КВАДРАТНІ Рівняння ... 4. і дослідження квадратних рівнянь ... 4 .. Квадратне рівняння з числовими коефіцієнтами ... 4 .. Вирішити і досліджувати квадратні рівняння щодо
РОЗДІЛ ЗАВДАННЯ З ПАРАМЕТРАМИ Коментар Завдання з параметрами традиційно є складними завданнями в структурі ЄДІ, які вимагають від абітурієнта не тільки володіння всіма методами і прийомами вирішення різних
Диференціальне числення Введення в математичний аналіз Межа послідовності і функції. Розкриття невизначеностей в межах. Похідна функції. Правила диференціювання. застосування похідної
Ряди Фур'є Ортогональні системи функцій З точки зору алгебри рівність де - функції даного класу а - коефіцієнти з R або C просто означає що вектор є лінійною комбінацією векторів В
1. Визначений інтеграл 1.1. Нехай f обмежена функція, задана на відрізку [, b] R. розбиття відрізка [, b] називають такий набір точок τ \u003d (x, x 1, ..., x n 1, x n) [, b], що \u003d x< x 1 < < x n 1
Гл Статечні ряди a a a Ряд виду a a a a a () називається статечним, де, a, постійні, звані коефіцієнтами ряду Іноді розглядають статечної ряд більш загального вигляду: a a (a) a (a) a (a) (), де
слід:1) намалювати графік f (x) на проміжку хоча б довжиною в два періоди, щоб показати, що дана функція періодична;
2) намалювати графік S (x) аналогічно, щоб було видно в яких точках f (x) ¹S (x);
3) обчислити коефіцієнти Фур'є і записати ряд Фур'є.
завдання
№1. Розкласти в ряд Фур'є
Рішення. Зауважимо, що f (x) задана на проміжку довжини T \u003d 4. Оскільки f (x) передбачається періодичної, то саме це число і є її періодом, тоді - l \u003d 2.
1) Графік f (x):
2) Графік S (x):
Стрілки в кінцях ліній показують, що функція не приймає в кінцях інтервалу значення, що визначається з виразу, заданого на інтервалі. При порівнянні графіків f (x) і S (x) добре видно, що в точках розриву f (x) ¹S (x).
3) Обчислимо коефіцієнти Фур'є. Це можна зробити за формулами (3 *):; ; . Саме:; отже,
розкладання f (x) в ряд Фур'є має вигляд:
Зауваження. 1) При інтегруванні на [-1;3] цей відрізок був розбитий на і , Тому що на цих відрізках f (x) задана різними значеннями.
2) При обчисленні коефіцієнтів використані інтеграли: і, де a \u003d const.
№2 . Розкласти в ряд Фур'є
Рішення. тут T \u003d 2, l \u003d 1.
Ряд Фур'є має вигляд:, де; ; , Тому що l \u003d 1.
1) Графік f (x):
2) Графік S (x):
№3. Розкласти в ряд Фур'є по синусах
Рішення. Зауважимо, що в ряд Фур'є по синусах розкладаються тільки непарні функції. Оскільки f (x) визначена тільки для x\u003e 0, xÎ (0; 2) È (2; 3), То це означає, що на симетричний проміжок (-3; -2) È (-2; 0) f (x)потрібно продовжити так, щоб виконувалася рівність f (-x) \u003d -f (x). Тому довжина проміжку, на якому f (x) задана як непарна функція, дорівнює 6. Значить T \u003d 6, l \u003d 3. Ряд Фур'є для f (x) має вигляд:, де, n \u003d 1, 2, 3, (за формулами (5 ")).
1) Графік f (x).
Щоб намалювати графік f (x) як непарної функції, намалюємо спочатку графік на (0; 2) È (2; 3), А потім скористаємося тим, що графік непарної функції симетричний відносно початку координат. З цих міркувань отримуємо графік f (x) на (-3; -2) È (-2; 0). потім продовжуємо f (x) T \u003d 6.
2) Графік S (x).
Графік S (x) відрізняється від графіка f (x) в точках розриву функції f (x). Наприклад, в т. x \u003d 2 f (x)не визначена, а S (x) має при x \u003d 2 значення, рівне напівсума односторонніх меж функції f (x), Саме: , Де,.
Отже,, тоді розкладання f (x) в ряд Фур'є має вигляд:.
№4 . Розкласти в ряд Фур'є по косинусам.
Рішення. Зауважимо, що в ряд Фур'є по косинусам розкладаються тільки парні функції. Оскільки f (x) задана тільки для x\u003e 0, xÎ (0; 2) È (2; 3], то це означає, що на симетричний проміжок [-3; -2) È (-2; 0) f (x)потрібно продовжити так, щоб виконувалося рівність: f (-x) \u003d f (x). Тому довжина проміжку, на якому f (x) задана як парна функція, дорівнює 6, тоді T \u003d 6, l \u003d 3. Ряд Фур'є в цьому випадку має вигляд:
де; ; n \u003d 1,2, ... (За формулами (4 ")).
1) Графік f (x).
Щоб намалювати графік f (x) як парної функції, намалюємо спочатку графік f (x) на (0; 2) È (2; 3], А потім скористаємося тим, що графік парної функції симетричний щодо осі ординат. З цих міркувань отримуємо графік f (x) на [-3; -2) È (-2; 0). потім продовжуємо f (x) на всю числову пряму як періодичну функцію з періодом T \u003d 6.
тут графік f (x) намальований на двох повних періодах функції.
2) Графік S (x).
Графік S (x) відрізняється від графіка f (x) в точках розриву функції f (x). Наприклад, в т. x \u003d 0 f (x)не визначена, а S (x) має значення: , Тому графік S (x) не переривається в т. x \u003d 0, На відміну від графіка f (x).
розкладання f (x) в ряд Фур'є по косинусам має вигляд:.
№5. Розкласти в ряд Фур'є f (x) \u003d | x |, xÎ (-2; 2)..
Рішення. За умовою, f (x) є парною функцією на (-2;2) ; тобто її ряд Фур'є містить тільки косинуси, при цьому T \u003d 4, l \u003d 2, ,
де; ; n \u003d 1, 2,
1) Графік f (x):
2) Графік S (x):
3), тому що | X | \u003d xдля x\u003e 0.; .
тоді розкладання f (x) в ряд Фур'є має вигляд:. Зауважимо, що при інтегруванні виразів або застосовується формула інтегрування частинами:, де u \u003d x; dv \u003d cos (ax) dxабо dv \u003d sin (ax) dx.
№6. Розкласти функцію в ряд Фур'є: а) в інтервалі (- ?,?); б) в інтервалі (0, 2?); в) в інтервалі (0,?) в ряд синусів.
Рішення. а) Графік функції з 2? - періодичним продовженням має вигляд
Функція задовольняє умовам теореми Діріхле і тому її можна розкласти в ряд Фур'є.
Обчислимо коефіцієнти Фур'є. Так як функція парна, то bn \u003d 0 (n \u003d 0, 1, 2, ...) і (n \u003d 0, 1, 2, ...).
Для обчислення цього інтеграла застосовують формулу інтегрування частинами у визначеному інтегралі. отримуємо
Ряд Фур'є даної функції має вигляд. В силу ознаки Діріхле даний ряд представляє функцію х2 в інтервалі (-?,?).
б) Інтервал (0, 2?) не симетричний відносно початку координат, а довжина його 2 l \u003d 2 ?. Обчислюємо коефіцієнти Фур'є за формулами:
Тому ряд Фур'є має вигляд. В силу теореми Діріхле ряд сходиться до породжує функції в точках х? (0,2?), А в точках 0 і 2? до значення. Графік суми ряду має вигляд
в) Функція, що розкладається в ряд по синусах, повинна бути непарною. Отже, довизначити задану функцію х2 в (-π, π) непарних чином, тобто розглядаємо функцію. Для цієї функції f (x) маємо аn \u003d 0 (n \u003d 0, 1, 2, ...) і
Шукане розкладання має вигляд.
Графік суми ряду має вигляд
Відзначимо, що в точках х \u003d (-π, π) ряд Фур'є сходиться до нуля.
№7 Розкласти в ряд Фур'є функцію, задану графічно:
Рішення . Отримаємо явне вираз для f (x). Графік функції - пряма лінія, використовуємо рівняння прямої у вигляді. Як видно з креслення,, тобто f (x) \u003d x - 1 (-1< x < 1) и период Т = 2.
Ця функція задовольняє умовам ознаки Діріхле, тому вона розкладається в ряд Фур'є. Обчислимо коефіцієнти Фур'є ( l = 1):
; (N \u003d 1, 2, ...);
Ряд Фур'є для функції f (x) має вигляд
Він являє функцію f (x) при -1< x < 1, а в точках х0 = -1 и х0 = 1 ряд сходится к -1.
№8. Розкласти функцію в тригонометричний ряд Фур'є на відрізку і вказати функцію, до якої сходиться отриманий ряд.
Рішення.Намалювати графік функції, продовживши її періодично з періодом або на всю вісь. Продовжена функція має період.
Перевірити умови достатніх ознак збіжності ряду Фур'є (Діні-Ліпшиця, Жордана, Діріхле).
Функція кусочно-монотонна на відрізку: вона зростає на і на. У точках функція має розриви першого роду.
З'ясувати парність або непарність функції: Функція не є ні парною, ні непарною.
а) якщо функція задана на
б) якщо функція задана на
Скласти ряд Фур'є функції:.
Вказати функцію, до якої буде сходитися цей ряд, користуючись поточечной ознаками збіжності: Згідно ознакою Дирихле ряд Фур'є функції сходиться до суми:
№9. Розкласти функцію, в ряд Фур'є по синусах на і за допомогою цього розкладання знайти суму числового ряду.
Рішення.Продовжити функцію парних (непарних) чином на (- p, 0) або (- l, 0), а потім періодично з періодом 2 p або 2 l продовжити функцію на всю вісь.
Продовжимо функцію непарних чином на, а потім періодично, з періодом, продовжимо її на всю вісь.
Намалювати графік періодичного продовження. Ми отримаємо функцію виду:
Перевірити умови достатніх ознак збіжності ряду Фур'є (Діні-Липиця, Жордана, Діріхле).
Функція кусочно-постійна в проміжку: вона дорівнює -1 на і 1 на. У точках функція має розриви першого роду.
Обчислити коефіцієнти Фур'є:
Її коефіцієнти Фур'є обчислюються за формулами:
Скласти ряд Фур'є функції. .
Вказати функцію, до якої буде сходитися цей ряд, користуючись поточечной ознаками збіжності.
Згідно ознакою Дирихле ряд Фур'є функції сходиться до суми:
Отже, при
Підставивши значення, вказати суму заданого числового ряду.
Вважаючи в отриманому розкладанні, знайдемо,
звідки, так як,.
№10. Написати рівність Парсеваля для функції, і, виходячи з цього рівності, знайти суму числового ряду.
Рішення.Встановити, чи є дана функція функцією з інтегрованим квадратом на.
Функція неперервна, а, отже, інтегрована на. З тієї ж причини її квадрат інтегруємо на.
Обчислити коефіцієнти Фур'є за формулами:
Так як непарна функція, то її коефіцієнти Фур'є обчислюються за формулами:
Обчислити інтеграл.
Написати формулу Парсеваля:
Таким чином, формула Парсеваля має вигляд
Провівши, якщо потрібно, арифметичні дії в правій і лівій частинах, отримати суму даного числового ряду.
Розділивши обидві частини отриманого рівності на 144, знайдемо:.
№11. Знайти інтеграл Фур'є функції
і побудувати його графік.
Рішення.Побудувати графік функції.
Перевірити виконання умов достатніх ознак збіжності інтеграла Фур'є (Діні, Діріхле-Жордана або наслідків з них).
Функція абсолютно інтегровна в проміжку, неперервна при і, а в точці має розрив першого роду. Далі, при і функція має кінцеву похідну, а в нулі існують кінцеві права і ліва похідні. З'ясувати парність або непарність функції. Функція не є ні парною, ні непарною. ; .
Отже,, або,
поруч Фур'є функції f (x) на інтервалі (-π; π) називається тригонометричний ряд виду:, де
Поруч Фур'є функції f (x) на інтервалі (-l; l) називається тригонометричний ряд виду: ![]() , де
, де
Призначення. онлайн калькулятор призначений для розкладання функції f (x) в Ряд Фур'є.
Для функцій по модулю (наприклад, | x |), використовуйте розкладання по косинусам.
Правила введення функцій:
Для функцій по модулю використовуйте розкладання по косинусам. Наприклад, для | x | необхідно ввести функцію без модуля, тобто x.Ряд Фур'є кусочно-безперервною, кусочно-монотонної й обмеженої на інтервалі (- l;l) Функції сходиться на всій числовій осі.
Сума ряду Фур'є S (x):
- є періодичною функцією з періодом 2 l. Функція u (x) називається періодичною з періодом T (або T-періодичної), якщо для всіх x області R, u (x + T) \u003d u (x).
- на інтервалі (- l;l) Збігається з функцією f(x), За винятком точок розриву
- в точках розриву (першого роду, тому що функція обмежена) функції f(x) І на кінцях інтервалу приймає середні значення:
Кажуть, що функція розкладається в ряд Фур'є на інтервалі (- l;l):
якщо f(x) - парна функція, то в її розкладанні беруть участь тільки парні функції, тобто b n=0.
якщо f(x) - непарна функція, то в її розкладанні беруть участь тільки непарні функції, тобто а n=0
поруч Фур'є
функції f(x) На інтервалі (0; l) по косинусам кратних дуг
називається ряд: ![]() , де
, де  .
.
поруч Фур'є
функції f(x) На інтервалі (0; l) по синусах кратних дуг
називається ряд: ![]() , де
, де  .
.
Сума ряду Фур'є по косинусам кратних дуг є парною періодичною функцією з періодом 2 l, Що збігається з f(x) На інтервалі (0; l) В точках безперервності.
Сума ряду Фур'є по синусах кратних дуг є непарною періодичною функцією з періодом 2 l, Що збігається з f(x) На інтервалі (0; l) В точках безперервності.
Ряд Фур'є для даної функції на даному інтервалі має властивість єдиності, тобто якщо розкладання отримана будь-яким іншим способом, ніж використання формул, наприклад, за допомогою підбору коефіцієнтів, то ці коефіцієнти збігаються з обчисленими за формулами.
Приклад №1. Розкласти функцію f (x) \u003d 1:
а) в повний ряд Фур'є на інтервалі(-π ;π);
б) в ряд по синусах кратних дуг на інтервалі(0;π); побудувати графік отриманого ряду Фур'є
Рішення:
а) Розкладання в ряд Фур'є на інтервалі (-π; π) має вигляд: ![]() ,
,
причому всі коефіцієнти b n\u003d 0, тому що дана функція - парна; таким чином,
Очевидно, рівність буде виконано, якщо прийняти
а 0 =2, а 1 =а 2 =а 3 =…=0
В силу властивості єдиності це і є шукані коефіцієнти. Таким чином, шукане розкладання: ![]() або просто 1 \u003d 1.
або просто 1 \u003d 1.
В такому випадку, коли ряд тотожно збігається зі своєю функцією, графік ряду Фур'є збігається з графіком функції на всій числовій прямій.
б) Розкладання на інтервалі (0; π) по синусах кратних дуг має вигляд:
Підібрати коефіцієнти так, щоб рівність тотожне виконувалося, очевидно, неможливо. Скористаємося формулою для обчислення коефіцієнтів:
Таким чином, для парних n (n=2k) маємо b n\u003d 0, для непарних ( n=2k-1) - ![]()
остаточно, ![]() .
.
Побудуємо графік отриманого ряду Фур'є, скориставшись його властивостями (див. Вище).
Перш за все, будуємо графік даної функції на заданому інтервалі. Далі, скориставшись непарні суми ряду, продовжуємо графік симетрично початку координат: 
Продовжуємо періодичним чином на всій числовій осі: 
І нарешті, в точках розриву заповнюємо середні (між правим і лівим межею) значення: 
Приклад №2. розкласти функцію ![]() на інтервалі (0; 6) по синусах кратних дуг.
на інтервалі (0; 6) по синусах кратних дуг.
Рішення: Шукане розкладання має вигляд:
Оскільки і ліва, і права частини рівності містять тільки функції sin від різних аргументів, слід перевірити, чи збігаються при будь-яких значеннях n (натуральних!) аргументи синусів в лівій і правій частинах рівності:
або, звідки n \u003d 18. Значить, таке доданок міститься в правій частині і коефіцієнт при ньому повинен збігатися з коефіцієнтом в лівій частині: b 18 =1;
або, звідки n \u003d 4. значить, b 4 =-5.
Таким чином, за допомогою підбору коефіцієнтів вдалося отримати шукане розкладання.


